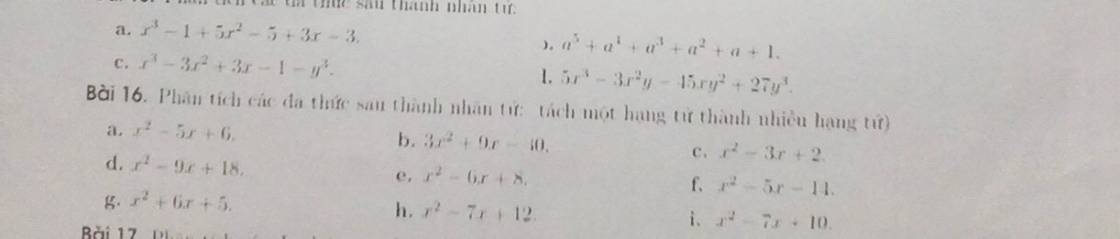Bài 16
a) \(=x^2-2x-3x+6\)
\(=x\left(x-2\right)-3\left(x-2\right)\)
\(=\left(x-3\right)\left(x-2\right)\)
c) \(=x^2-x-2x+2\)
\(=x\left(x-1\right)-2\left(x-1\right)=\left(x-2\right)\left(x-1\right)\)
d) \(=x^2-3x-6x+18\)
\(=x\left(x-3\right)-6\left(x-3\right)=\left(x-6\right)\left(x-3\right)\)
e) \(=x^2-2x-4x+8=x\left(x-2\right)-4\left(x-2\right)=\left(x-4\right)\left(x-2\right)\)
g) \(=x^2+x+5x+5=x\left(x+1\right)+5\left(x+1\right)=\left(x+5\right)\left(x+1\right)\)
h) \(=x^2-3x-4x+12=x\left(x-3\right)-4\left(x-3\right)=\left(x-4\right)\left(x-3\right)\)
i) \(=x^2+2x+5x+10=x\left(x+2\right)+5\left(x+2\right)=\left(x+5\right)\left(x+2\right)\)
f) \(=x^2+2x-7x-14=x\left(x+2\right)-7\left(x+2\right)=\left(x-7\right)\left(x+2\right)\)