Question

Answer 1

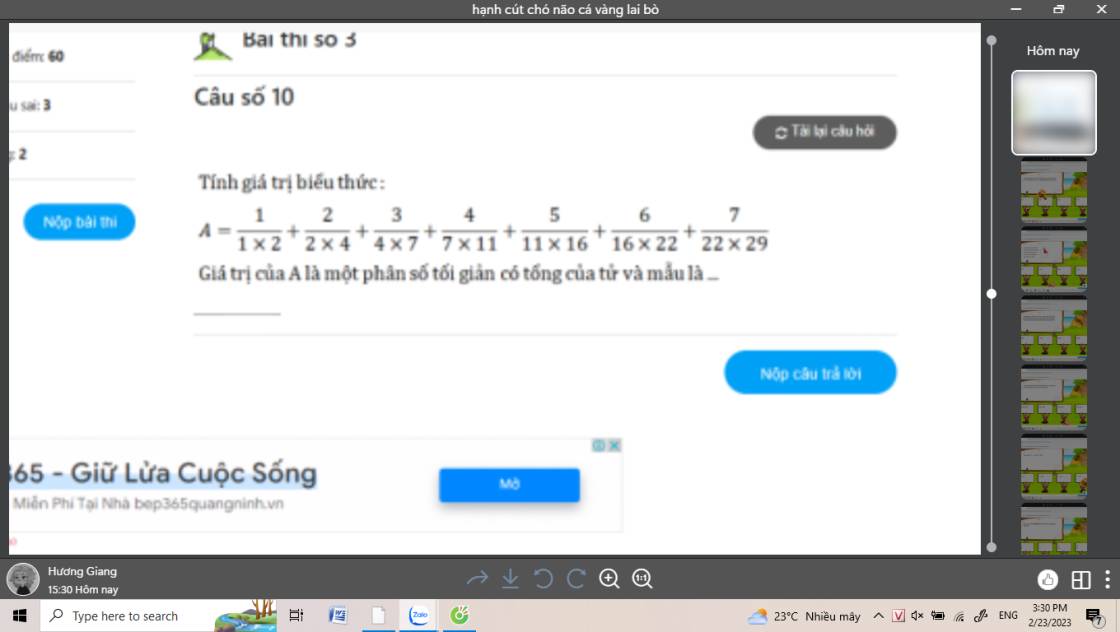
\(A=\dfrac{1}{1\times2}+\dfrac{2}{2\times4}+\dfrac{3}{4\times7}+\dfrac{4}{7\times11}+\dfrac{5}{11\times16}+\dfrac{6}{16\times22}+\dfrac{7}{22\times29}\\ =\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{22}+\dfrac{1}{22}-\dfrac{1}{29}\\ =\dfrac{1}{1}-\dfrac{1}{29}\\ =\dfrac{29}{29}-\dfrac{1}{29}\\ =\dfrac{28}{29}\)

Giá trị của `A` là một phân số tối giản có tổng của từ và mẫu là `28+29=57`