5.
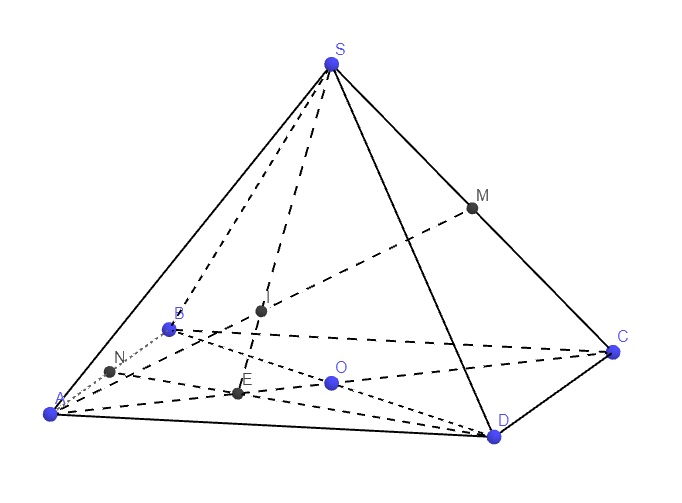
Gọi giao điểm AC và BD là O
\(\Rightarrow\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Qua S kẻ đường thẳng d song song AB và CD
Do \(\left\{{}\begin{matrix}AB\in\left(SAB\right)\\CD\in\left(SCD\right)\\AB||CD\\S\in\left(SAB\right)\cap\left(SCD\right)\end{matrix}\right.\) \(\Rightarrow\) giao tuyến (SAB) và (SCD) là đường thẳng qua S và song song AB, CD
\(\Rightarrow d=\left(SAB\right)\cap\left(SCD\right)\)
b.
Trong mp (ABCD), gọi E là giao điểm DN và AC \(\Rightarrow E\in\left(SAC\right)\cap\left(SND\right)\)
Trong mp (SAC), nối AM cắt SE tại I
\(\Rightarrow I=AM\cap\left(SND\right)\)
Đặt \(\dfrac{AI}{AM}=x\Rightarrow\overrightarrow{AI}=x.\overrightarrow{AM}\)
Do N là trung điểm AB, O là trung điểm BD \(\Rightarrow\) E là trọng tâm tam giác ABD
\(\Rightarrow\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AO}=\dfrac{2}{3}.\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AC}\)
\(\overrightarrow{SI}=\overrightarrow{SA}+\overrightarrow{AI}=\overrightarrow{SA}+x.\overrightarrow{AM}=\overrightarrow{SA}+x\left(\dfrac{1}{2}\overrightarrow{AS}+\dfrac{1}{2}\overrightarrow{AC}\right)=\left(1-\dfrac{x}{2}\right)\overrightarrow{SA}+\dfrac{x}{2}\overrightarrow{AC}\)
\(\overrightarrow{SE}=\overrightarrow{SA}+\overrightarrow{AE}=\overrightarrow{SA}+\dfrac{1}{3}\overrightarrow{AC}\)
Do S, I, E thẳng hàng:
\(\Rightarrow\left(1-\dfrac{x}{2}\right):1=\dfrac{x}{2}:\dfrac{1}{3}\Rightarrow x=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AI}{AM}=\dfrac{1}{2}\)