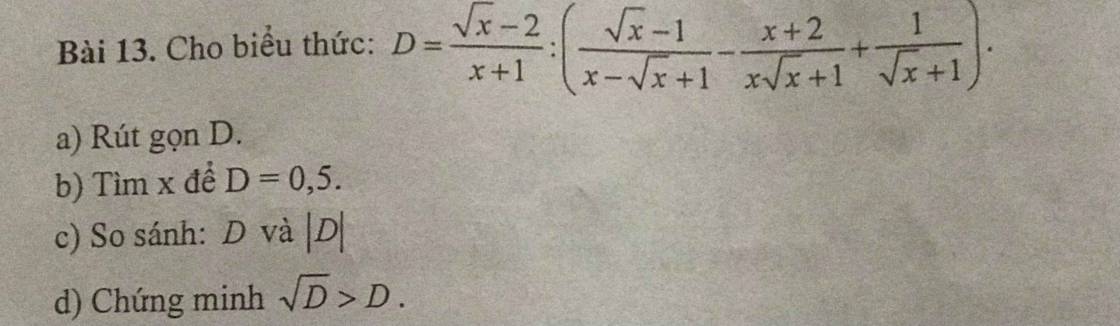a: \(D=\dfrac{\sqrt{x}-2}{x+1}:\dfrac{x-1-x-2+x-\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-2}{x+1}\cdot\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}-2}\)
\(=\dfrac{x-\sqrt{x}+1}{x+1}\)
b Để D=0,5 thì \(x-\sqrt{x}+1=\dfrac{1}{2}x+\dfrac{1}{2}\)
=>\(\dfrac{1}{2}x-\sqrt{x}+\dfrac{1}{2}=0\)
=>\(x-2\sqrt{x}+1=0\)
=>x=1(loại)
c: \(\left\{{}\begin{matrix}x-\sqrt{x}+1>0\\x+1>0\end{matrix}\right.\)
=>D>0
=>D>=|D|
Đúng 0
Bình luận (0)
