\(B=\dfrac{3}{1.3}+\dfrac{3}{3.5}+\dfrac{3}{5.7}+...+\dfrac{3}{49.51}\)
\(B=\dfrac{2}{3}.\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{49.51}\right)\)
\(B=\dfrac{3}{2}.\left(\dfrac{3-1}{1.3}+\dfrac{5.3}{3.5}+\dfrac{7-5}{5.7}+...+\dfrac{51-49}{49.51}\right)\)
\(B=\dfrac{3}{2}.\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{49}-\dfrac{1}{51}\right)\)
\(B=\dfrac{3}{2}.\left(1-\dfrac{1}{51}\right)\)
\(B=\dfrac{3}{2}.\dfrac{50}{51}\)
\(B=\dfrac{25}{17}\)


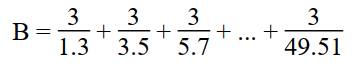








 4 và 5
4 và 5



