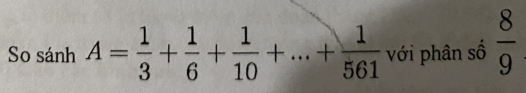Ta có:A=\(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{1}{561}\)
=\(\dfrac{1}{1.3}+\dfrac{1}{2.3}+\dfrac{1}{2.5}+...+\dfrac{1}{17.33}\)
⇒\(\dfrac{1}{2}A=\dfrac{1}{1.2.3}+\dfrac{1}{2.3.2}+\dfrac{1}{2.5.2}+...+\dfrac{1}{17.33.2}\)
=\(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{33.34}\)
=\(\dfrac{3-2}{2.3}+\dfrac{4-3}{3.4}+\dfrac{5-4}{4.5}+...+\dfrac{34-33}{33.34}\)
=\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{33}-\dfrac{1}{34}\)
=\(\dfrac{1}{2}-\dfrac{1}{34}\)
=\(\dfrac{8}{17}\)
⇒A=\(\dfrac{8}{17}:\dfrac{1}{2}=\dfrac{16}{17}\)
Vì \(\dfrac{16}{17}>\dfrac{8}{9}\) ⇒ A \(>\dfrac{8}{9}\)