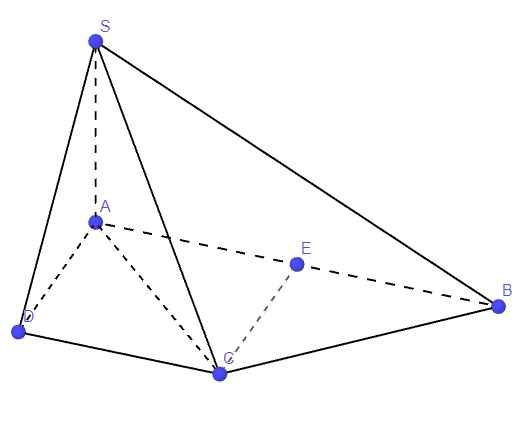
Gọi E là trung điểm AB \(\Rightarrow AE=EB=a\Rightarrow AECD\) là hình vuông
\(\Rightarrow CE=AD=a\Rightarrow BC=\sqrt{CE^2+BE^2}=a\sqrt{2}\)
\(AC=\sqrt{AD^2+CD^2}=a\sqrt{2}\)
\(\Rightarrow AC^2+BC^2=4a^2=AB^2\Rightarrow\Delta ABC\) vuông tại C hay \(BC\perp AC\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp\left(SAC\right)\)
Mà \(BC=\left(SAB\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SCA}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{1}{\sqrt{2}}\Rightarrow\widehat{SCA}=35^016'\)
Đúng 0
Bình luận (0)
