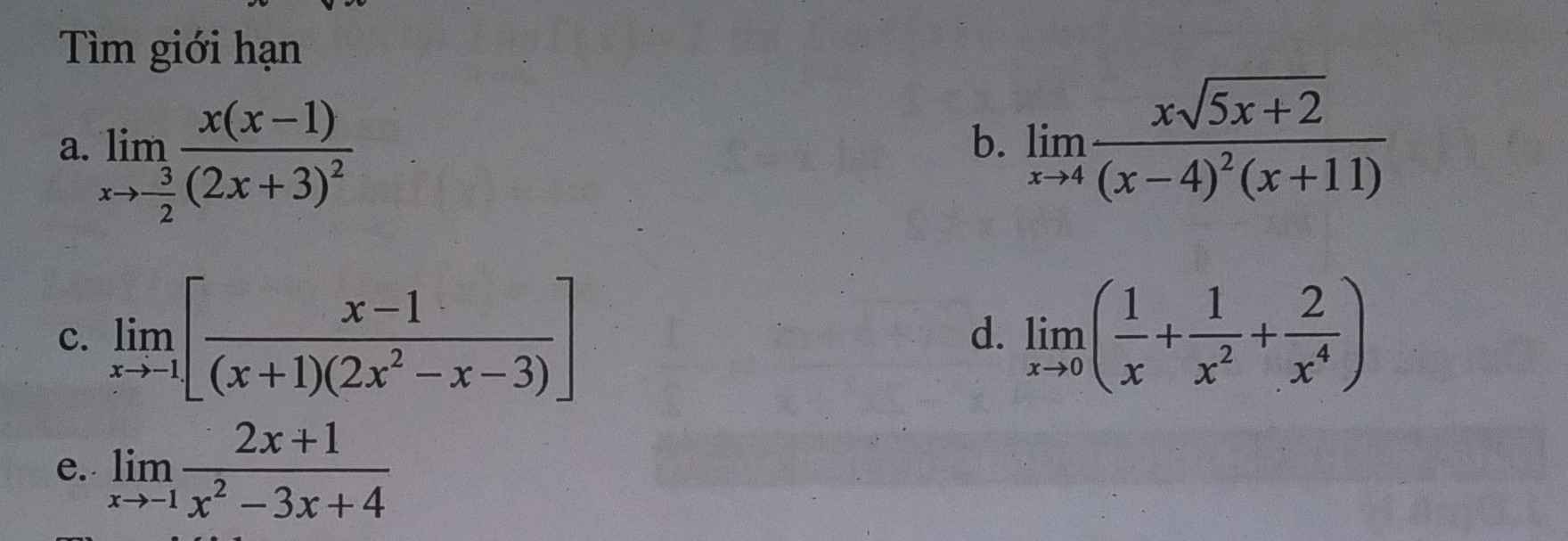a.
\(\lim\limits_{x\rightarrow-\dfrac{3}{2}}\dfrac{x\left(x-1\right)}{\left(2x+3\right)^2}=\dfrac{\dfrac{15}{4}}{0}=+\infty\)
b.
\(\lim\limits_{x\rightarrow4}\dfrac{x\sqrt{5x+2}}{\left(x-4\right)^2\left(x+11\right)}=\dfrac{2\sqrt{22}}{0}=+\infty\)
c.
\(\lim\limits_{x\rightarrow-1}\left[\dfrac{x-1}{\left(x+1\right)\left(2x^2-x-3\right)}\right]=\lim\limits_{x\rightarrow-1}\dfrac{\left(x-1\right)}{\left(x+1\right)^2\left(2x-3\right)}\)
\(=\lim\limits_{x\rightarrow-1}\dfrac{\dfrac{x-1}{2x-3}}{\left(x+1\right)^2}=\dfrac{\dfrac{2}{5}}{0}=+\infty\)
d.
\(\lim\limits_{x\rightarrow0}\left(\dfrac{1}{x}+\dfrac{1}{x^2}+\dfrac{2}{x^4}\right)=\lim\limits_{x\rightarrow0}\left(\dfrac{x^3+x^2+2}{x^4}\right)=\dfrac{2}{0}=+\infty\)
e.
\(\lim\limits_{x\rightarrow-1}\dfrac{2x+1}{x^2-3x+4}=\dfrac{-1}{8}\)