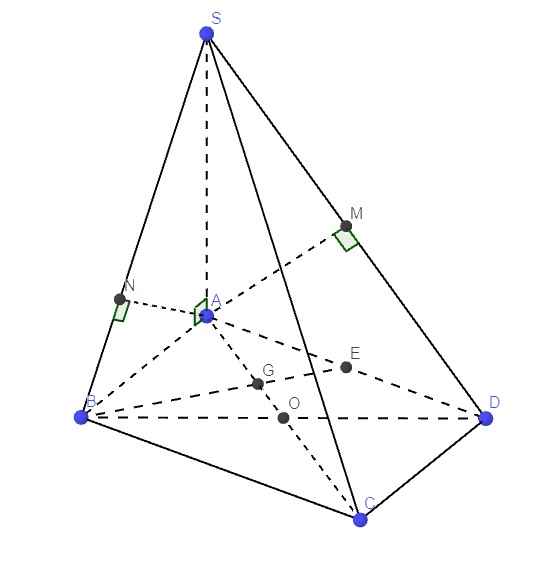
a.
Do G là trọng tâm tam giác ABD \(\Rightarrow\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{DG}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SD}=\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SD}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GD}\)
\(=\left(\overrightarrow{SA}+\overrightarrow{AG}\right)+\left(\overrightarrow{SB}+\overrightarrow{BG}\right)+\left(\overrightarrow{SD}+\overrightarrow{DG}\right)\)
\(=3\overrightarrow{SG}\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AN\)
Mà \(AN\perp SB\Rightarrow AN\perp\left(SBC\right)\)
c.
Hoàn toàn tương tự câu b, ta có \(AM\perp\left(SCD\right)\Rightarrow AM\perp SC\)
Mà \(AN\perp\left(SBC\right)\Rightarrow AN\perp SC\)
\(\Rightarrow SC\perp\left(AMN\right)\Rightarrow SC\perp MN\)