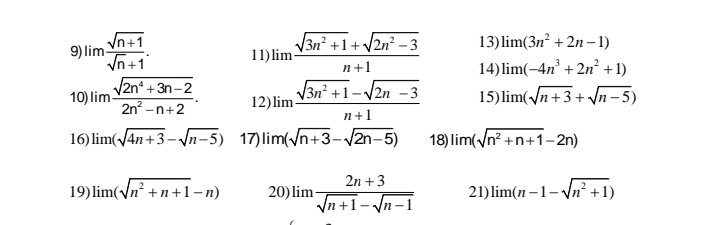9.
\(\lim\dfrac{\sqrt{n+1}}{\sqrt{n}+1}=\lim\dfrac{\sqrt{n}\left(\sqrt{1+\dfrac{1}{n}}\right)}{\sqrt{n}\left(1+\dfrac{1}{\sqrt{n}}\right)}=\lim\dfrac{\sqrt{1+\dfrac{1}{n}}}{1+\dfrac{1}{\sqrt{n}}}=\dfrac{\sqrt{1+0}}{1+\sqrt{0}}=1\)
10.
\(\lim\dfrac{\sqrt{2n^4+3n-2}}{2n^2-n+2}=\lim\dfrac{n^2\left(\sqrt{2+\dfrac{3}{n^3}-\dfrac{2}{n^4}}\right)}{n^2\left(2-\dfrac{1}{n}+\dfrac{2}{n^2}\right)}\)
\(=\lim\dfrac{\sqrt{2+\dfrac{3}{n^3}-\dfrac{2}{n^4}}}{2-\dfrac{1}{n}+\dfrac{2}{n^2}}=\dfrac{\sqrt{2+0-0}}{2-0+0}=\dfrac{\sqrt{2}}{2}\)
11.
\(lim\dfrac{\sqrt{3n^2+1}+\sqrt{2n^2-3}}{n+1}=\lim\dfrac{n\sqrt{3+\dfrac{1}{n^2}}+n\sqrt{2-\dfrac{3}{n^2}}}{n\left(1+\dfrac{1}{n}\right)}\)
\(=\lim\dfrac{\sqrt{3+\dfrac{1}{n^2}}+\sqrt{2-\dfrac{3}{n^2}}}{1+\dfrac{1}{n}}=\dfrac{\sqrt{3}+\sqrt{2}}{1}=\sqrt{3}+\sqrt{2}\)
12.
\(\lim\dfrac{\sqrt{3n^2+1}-\sqrt{2n-3}}{n+1}=\lim\dfrac{n\sqrt{3+\dfrac{1}{n^2}}-n\sqrt{\dfrac{2}{n}-\dfrac{3}{n^2}}}{n\left(1+\dfrac{1}{n}\right)}\)
\(=\lim\dfrac{\sqrt{3+\dfrac{1}{n^2}}-\sqrt{\dfrac{2}{n}-\dfrac{3}{n^2}}}{1+\dfrac{1}{n}}=\dfrac{\sqrt{3+0}-\sqrt{0-0}}{1+0}=\sqrt{3}\)
13.
\(\lim\left(3n^2+2n-1\right)=\lim n^2\left(3+\dfrac{2}{n}-\dfrac{1}{n^2}\right)\)
Do \(\lim n^2=+\infty\)
\(\lim\left(3+\dfrac{2}{n}-\dfrac{1}{n^2}\right)=3+0-0=3>0\)
\(\Rightarrow\lim n^2\left(3+\dfrac{2}{n}-\dfrac{1}{n^2}\right)=+\infty\)
14.
\(\lim\left(-4n^3+2n^2+1\right)=\lim n^3\left(-4+\dfrac{2}{n}+\dfrac{1}{n^3}\right)\)
Do \(\lim\limits n^3=+\infty\)
\(\lim\left(-4+\dfrac{2}{n}+\dfrac{1}{n^3}\right)=-4+0+0=-4< 0\)
\(\Rightarrow\lim n^3\left(-4+\dfrac{2}{n}+\dfrac{1}{n^3}\right)=-\infty\)
15.
\(\lim\left(\sqrt{n+3}+\sqrt{n-5}\right)=\lim\sqrt{n}\left(\sqrt{1+\dfrac{3}{n}}+\sqrt{1-\dfrac{5}{n}}\right)\)
Do \(\lim\limits\sqrt{n}=+\infty\)
\(\lim\left(\sqrt{1+\dfrac{3}{n}}+\sqrt{1-\dfrac{5}{n}}\right)=2>0\)
\(\Rightarrow\lim\sqrt{n}\left(\sqrt{1+\dfrac{3}{n}}+\sqrt{1-\dfrac{5}{n}}\right)=+\infty\)
16.
\(\lim\left(\sqrt{4n+3}-\sqrt{n-5}\right)=\lim\sqrt{n}\left(\sqrt{4+\dfrac{3}{n}}-\sqrt{1-\dfrac{5}{n}}\right)\)
Do \(\lim\sqrt{n}=+\infty\)
\(\lim\left(\sqrt{4+\dfrac{3}{n}}-\sqrt{1-\dfrac{5}{n}}\right)=\sqrt{4}-\sqrt{1}=1>0\)
\(\Rightarrow\lim\sqrt{n}\left(\sqrt{4+\dfrac{3}{n}}-\sqrt{1-\dfrac{5}{n}}\right)=+\infty\)
17.
\(\lim\left(\sqrt{n+3}-\sqrt{2n-5}\right)=\lim\sqrt{n}\left(\sqrt{1+\dfrac{3}{n}}-\sqrt{2-\dfrac{5}{n}}\right)\)
Do \(\lim\sqrt{n}=+\infty\)
\(\lim\left(\sqrt{1+\dfrac{3}{n}}-\sqrt{2-\dfrac{5}{n}}\right)=1-\sqrt{2}< 0\)
\(\Rightarrow\lim\sqrt{n}\left(\sqrt{1+\dfrac{3}{n}}-\sqrt{2-\dfrac{5}{n}}\right)=-\infty\)
18.
\(\lim\left(\sqrt{n^2+n+1}-2n\right)=\lim n\left(\sqrt{1+\dfrac{1}{n}+\dfrac{1}{n^2}}-2\right)\)
Do \(\lim\left(n\right)=+\infty\)
\(\lim\left(\sqrt{1+\dfrac{1}{n}+\dfrac{1}{n^2}}-2\right)=1-2=-1< 0\)
\(\Rightarrow\lim n\left(\sqrt{1+\dfrac{1}{n}+\dfrac{1}{n^2}}-2\right)=-\infty\)
19.
\(\lim\left(\sqrt{n^2+n+1}-n\right)=\lim\dfrac{\left(\sqrt{n^2+n+1}-n\right)\left(\sqrt{n^2+n+1}+n\right)}{\sqrt{n^2+n+1}+n}\)
\(=\lim\dfrac{n+1}{\sqrt{n^2+n+1}+n}=\lim\dfrac{n\left(1+\dfrac{1}{n}\right)}{n\left(\sqrt{1+\dfrac{1}{n}+\dfrac{1}{n^2}}+1\right)}\)
\(=\lim\dfrac{1+\dfrac{1}{n}}{\sqrt{1+\dfrac{1}{n}+\dfrac{1}{n^2}}+1}=\dfrac{1+0}{\sqrt{1+0+0}+1}=\dfrac{1}{2}\)
20.
\(\lim\dfrac{2n+3}{\sqrt{n+1}-\sqrt{n-1}}=\lim\dfrac{\left(2n+3\right)\left(\sqrt{n+1}+\sqrt{n-1}\right)}{\left(\sqrt{n+1}-\sqrt{n-1}\right)\left(\sqrt{n+1}+\sqrt{n-1}\right)}\)
\(=\lim\dfrac{\left(2n+3\right)\left(\sqrt{n+1}+\sqrt{n-1}\right)}{2}\)
\(=\lim\dfrac{n\left(2+\dfrac{3}{n}\right).\sqrt{n}\left(\sqrt{1+\dfrac{1}{n}}+\sqrt{1-\dfrac{1}{n}}\right)}{2}\)
\(=\lim n\sqrt{n}.\dfrac{\left(2+\dfrac{3}{n}\right)\left(\sqrt{1+\dfrac{1}{n}}+\sqrt{1-\dfrac{1}{n}}\right)}{2}\)
Do \(\lim n\sqrt{n}=+\infty\)
\(\lim\dfrac{\left(2+\dfrac{3}{n}\right)\left(\sqrt{1+\dfrac{1}{n}}+\sqrt{1-\dfrac{1}{n}}\right)}{2}=\dfrac{2.2}{2}=2>0\)
\(\Rightarrow\lim n\sqrt{n}.\dfrac{\left(2+\dfrac{3}{n}\right)\left(\sqrt{1+\dfrac{1}{n}}+\sqrt{1-\dfrac{1}{n}}\right)}{2}=+\infty\)
21.
\(\lim\left(n-1-\sqrt{n^2+1}\right)=\lim\left(\dfrac{\left(n-\sqrt{n^2+1}\right)\left(n+\sqrt{n^2+1}\right)}{n+\sqrt{n^2+1}}-1\right)\)
\(=\lim\left(\dfrac{-1}{n+\sqrt{n^2+1}}-1\right)\)
\(=\lim\left(\dfrac{-1}{n\left(1+\sqrt{1+\dfrac{1}{n^2}}\right)}-1\right)\)
\(=\lim\left(\dfrac{-\dfrac{1}{n}}{1+\sqrt{1+\dfrac{1}{n^2}}}-1\right)=\dfrac{-0}{1+\sqrt{1+0}}-1=-1\)