Question

Answer 1

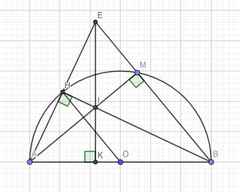
Đề bài sai, chắc đề đúng là "đường tròn tâm O đường kính AB".

Do AB là đường kính \(\Rightarrow\widehat{AHB}\)  là góc nội tiếp chắn nửa đường tròn

\(\Rightarrow\widehat{AHB}=90^0\)

\(\Rightarrow\) Hai điểm K và H cùng nhìn AI dưới 1 góc vuông

\(\Rightarrow\) Bốn điểm A,K,I,H cùng thuộc đường tròn đường kính AI

b.

Do H là điểm chính giữa cung AM \(\Rightarrow sđ\stackrel\frown{AH}=sđ\stackrel\frown{HM}\)

\(\Rightarrow\widehat{ABH}=\widehat{HBM}\) (hai góc nội tiếp chắn 2 cung bằng nhau)

\(\Rightarrow BH\) là phân giác của góc ABE

Mà \(BH\perp AH\Rightarrow BH\) vừa là đường cao, vừa là phân giác của tam giác BAE

\(\Rightarrow\Delta BAE\) cân tại B

Trong tam giác BAE, ta có I là giao điểm 2 đường cao AM và BH

\(\Rightarrow\) I là trực tâm tam giác BAE

Mặt khác \(IK\perp AB\Rightarrow\) đường thẳng IK là 1 đường cao của tam giác BAE

\(\Rightarrow IK\) đi qua E hay 3 điểm E, I, K thẳng hàng

Answer 2

Answer 3

1.

Gọi vận tốc từ A đến B của người đó là x>0 (km/h)

Vận tốc về từ B đến A: \(x+4\) (km/h)

Thời gian đi: \(\dfrac{24}{x}\) giờ

Thời gian về: \(\dfrac{24}{x+4}\) giờ

Do thời gian về ít hơn thời gian đi là \(\dfrac{1}{2}\) giờ nên ta có pt:

\(\dfrac{24}{x}-\dfrac{24}{x+4}=\dfrac{1}{2}\)

\(\Rightarrow48\left(x+4\right)-48x=x\left(x+4\right)\)

\(\Leftrightarrow x^2+4x-192=0\Rightarrow\left[{}\begin{matrix}x=12\\x=-16\left(loại\right)\end{matrix}\right.\)

Answer 4

2.

Gọi vận tốc của người đó khi đi từ A đến B là x>0 (km/h)

Vận tốc lúc về là: \(x+9\) (km/h)

Thời gian đi: \(\dfrac{90}{x}\) giờ

Thời gian về: \(\dfrac{90}{x+9}\) giờ

Theo bài ra ta có pt:

\(\dfrac{90}{x}+\dfrac{90}{x+9}+\dfrac{1}{2}=5\)

\(\Leftrightarrow20\left(x+9\right)+20x=x\left(x+9\right)\)

\(\Leftrightarrow x^2-31x-180=0\Rightarrow\left[{}\begin{matrix}x=36\\x=-5\left(loại\right)\end{matrix}\right.\)

Answer 5

3.

Gọi vận tốc dự định của người đó là x>0 (km/h)

Vận tốc trên đoạn đường còn lại: \(x+2\) (km/h)

Thời gian dự định đi hết quãng đường: \(\dfrac{60}{x}\) giờ

Thời gian đi nửa đoạn đầu: \(\dfrac{30}{x}\) giờ

Thời gian đi nửa đoạn sau: \(\dfrac{30}{x+2}\) giờ

Ta có pt:

\(\dfrac{30}{x}+\dfrac{30}{x+2}+\dfrac{1}{2}=\dfrac{60}{x}\)

\(\Rightarrow\dfrac{30}{x}=\dfrac{x+62}{2\left(x+2\right)}\)

\(\Rightarrow x\left(x+62\right)=60\left(x+2\right)\)

\(\Rightarrow x^2+2x-120=0\Rightarrow\left[{}\begin{matrix}x=10\\x=-12\left(loại\right)\end{matrix}\right.\)