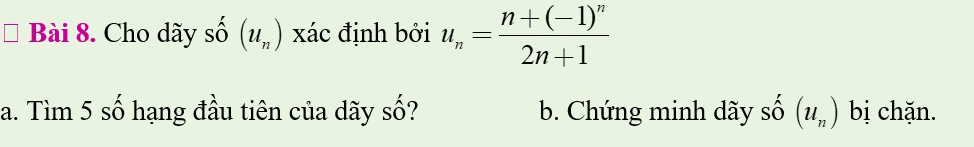Question

Answer 1

a, \(u_1=\dfrac{1+\left(-1\right)^1}{2.1+1}=0\)

\(u_2=\dfrac{3}{5}\)

\(u_3=\dfrac{2}{7}\)

\(u_4=\dfrac{5}{9}\)

\(u_5=\dfrac{4}{11}\)

Answer 2

b, Với \(n\in N^{\text{*}}\Rightarrow u_n=\dfrac{n+\left(-1\right)^n}{2n+1}>0\)

Với n chẵn, n có dạng \(2k\Rightarrow u_n=\dfrac{2k+1}{4k+1}< 1\)

Với n lẻ, n có dạng \(2k+1\Rightarrow u_n=\dfrac{2k+1-1}{4k+3}=\dfrac{2k}{4k+3}< 1\)

\(\Rightarrow\) Dãy số \(\left(u_n\right)\) bị chặn.