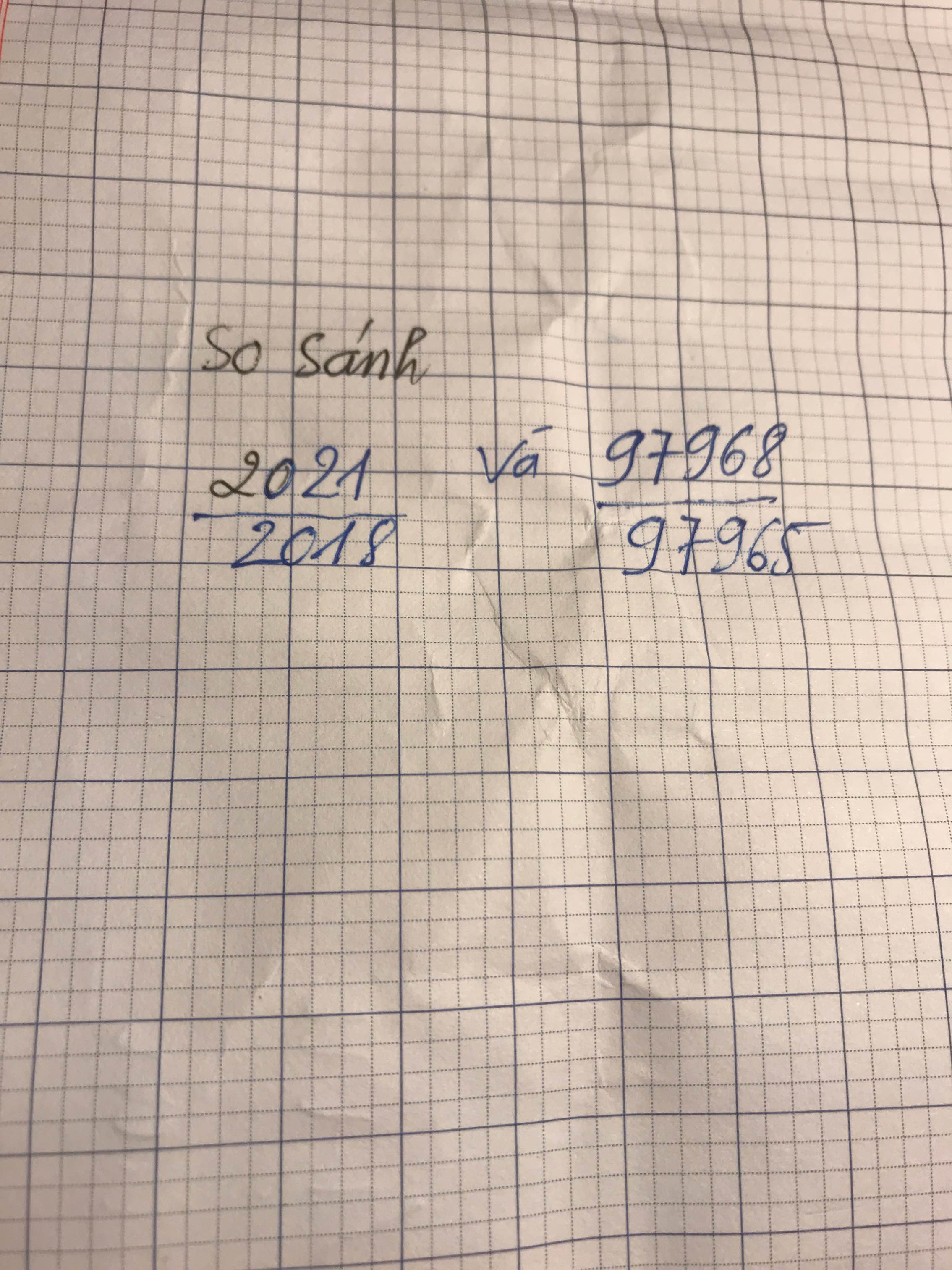Ta có:
\(\dfrac{2021}{2018}=\dfrac{2018+3}{2018}=1+\dfrac{3}{2018}\)
\(\dfrac{97968}{97965}=\dfrac{97965+3}{97965}=1+\dfrac{3}{97965}\)
Mà \(2018< 97965\) nên \(\dfrac{3}{2018}>\dfrac{3}{97965}\)
Từ đó suy ra \(1+\dfrac{3}{2018}>1+\dfrac{3}{97965}\) hay\(\dfrac{2021}{2018}>\dfrac{97968}{97965}\)
Cho dãy số sau:
3,89,175,.....
Hỏi số thứ 2795 là số nào?
Một ô tô đi từ tỉnh A đến tỉnh B. Mỗi giờ đi được 50 km. Biết rằng nếu ô tô đó đi được 12 quãng đường và 75 km thì còn phải di tiep14 quãng đường mới tới tỉnh B.Tính thời gian ô tô đi từ tỉnh A đến tỉnh B
tìm 2 số có hiệu bằng 603, biết nếu xóa chữ 9 ở hang đơn vị của số lớn thì được số bé
[_] 1
__ + 4 = ____
5 5
4 20 1
---- : ------- = ------
5 [_] 5
[_] là ô trống nhé! Giúp mình gấp!
Lớp 4A và lớp 4B của Trường Tiểu học Bình Minh quyên góp được 126 mảnh giấy vụn .Trong đó , số giấy vụn thu được của lớp 4A bằng 3/4 của lớp 4B . Hỏi mỗi lớp quyên góp được bao nhiêu kg giấy vụn ?
Một người bán trứng.ngay 1 bán đc 1\4 số trứng ngày 2 bán đc 2\5 số trứng thì còn lại 182 quả trứng .tính số trứng mỗi ngày người đó bán
Có hai vòi nước chảy vào cùng một bể. Nếu chỉ vòi thứ nhất chảy thì sau 12h nước sẽ đầy bể Nếu chỉ vòi thứ 2 chảy thì sau 4h nước sẽ đầy bể. Hỏi nếu cả hai vòi cùng chẩy thì sau bao lâu nước sẽ đầy bể
