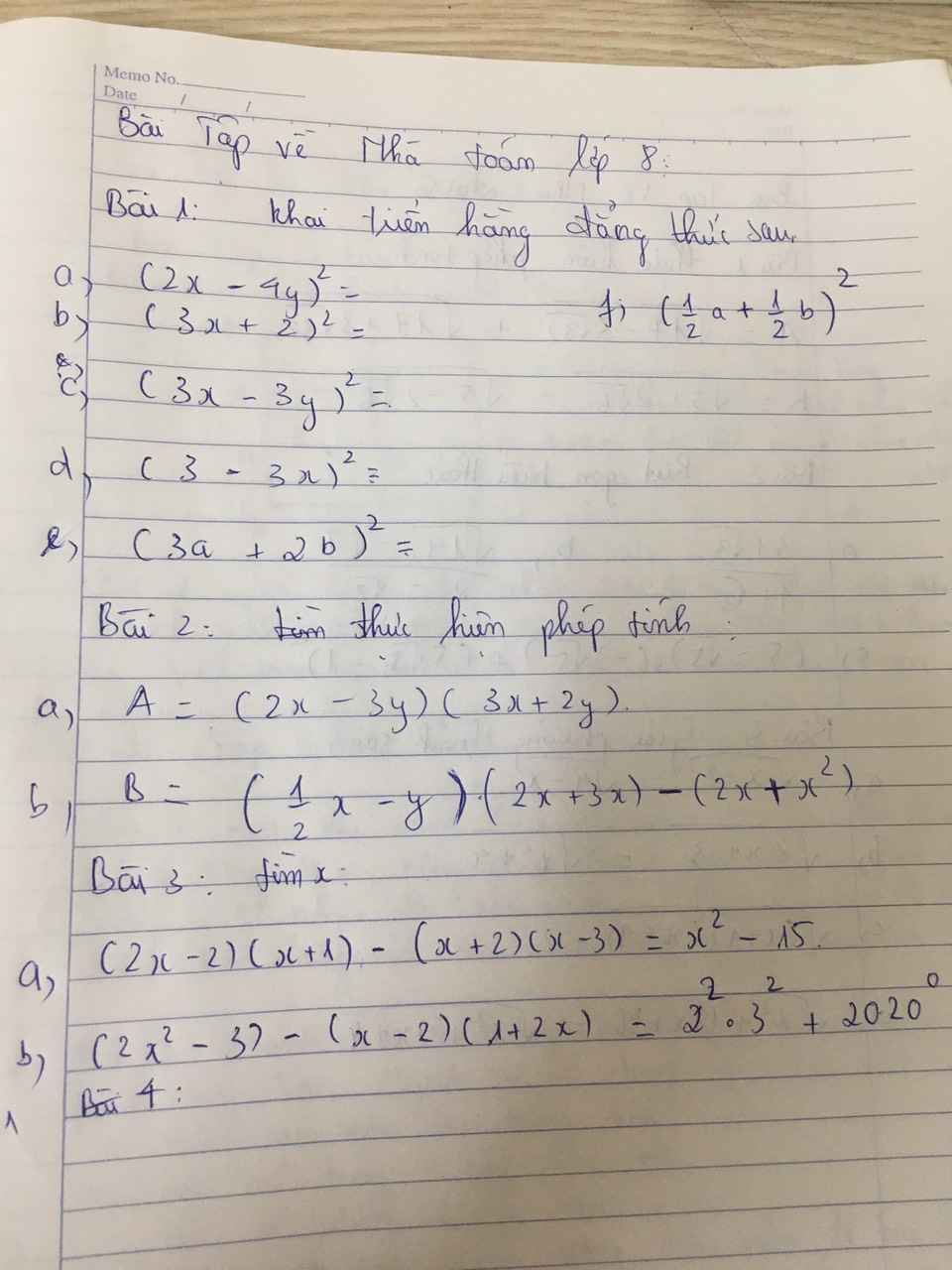Bài 2:
a) \(A=\left(2x-3y\right)\left(3x+2y\right)\\ =2x\left(3x+2y\right)-3y\left(3x+2y\right)\\ =6x^2+4xy-9xy-6y^2\\ =6x^2-5xy-6y^2\)
b) \(B=\left(\dfrac{1}{2}x-y\right)\left(2x+3x\right)-\left(2x+x^2\right)\\ =\left(\dfrac{1}{2}x-y\right).5x-2x-x^2\\ =\dfrac{5}{2}x^2-5xy-2x-x^2\\ =\dfrac{3}{2}x-5xy-x^2\)
Bài 1:
a) \(\left(2x-4y\right)^2=4x^2-16xy+16y^2\)
b) \(\left(3x+2\right)^2=9x^2+12x+4\)
c) \(\left(3x-3y\right)^2=9x^2-18xy+9y^2\)
d) \(\left(3-3x\right)^2=9-18x+9x^2\)
e) \(\left(3a+2b\right)^2=9a^2+12ab+4b^2\)
f) \(\left(\dfrac{1}{2}a+\dfrac{1}{2}b\right)^2=\dfrac{1}{4}a^2+\dfrac{1}{2}ab+\dfrac{1}{4}b^2\)
Bài 3:
a: Ta có: \(\left(2x-2\right)\left(x+1\right)-\left(x+2\right)\left(x-3\right)=x^2-15\)
\(\Leftrightarrow2x^2-2-x^2+x+6-x^2+15=0\)
\(\Leftrightarrow x+19=0\)
hay x=-19
b: Ta có: \(\left(2x^2-3\right)-\left(x-2\right)\left(2x+1\right)=2^2\cdot3^2+1\)
\(\Leftrightarrow2x^2-3-2x^2-x+4x+2=37\)
\(\Leftrightarrow3x=37+3-2=38\)
hay \(x=\dfrac{38}{3}\)