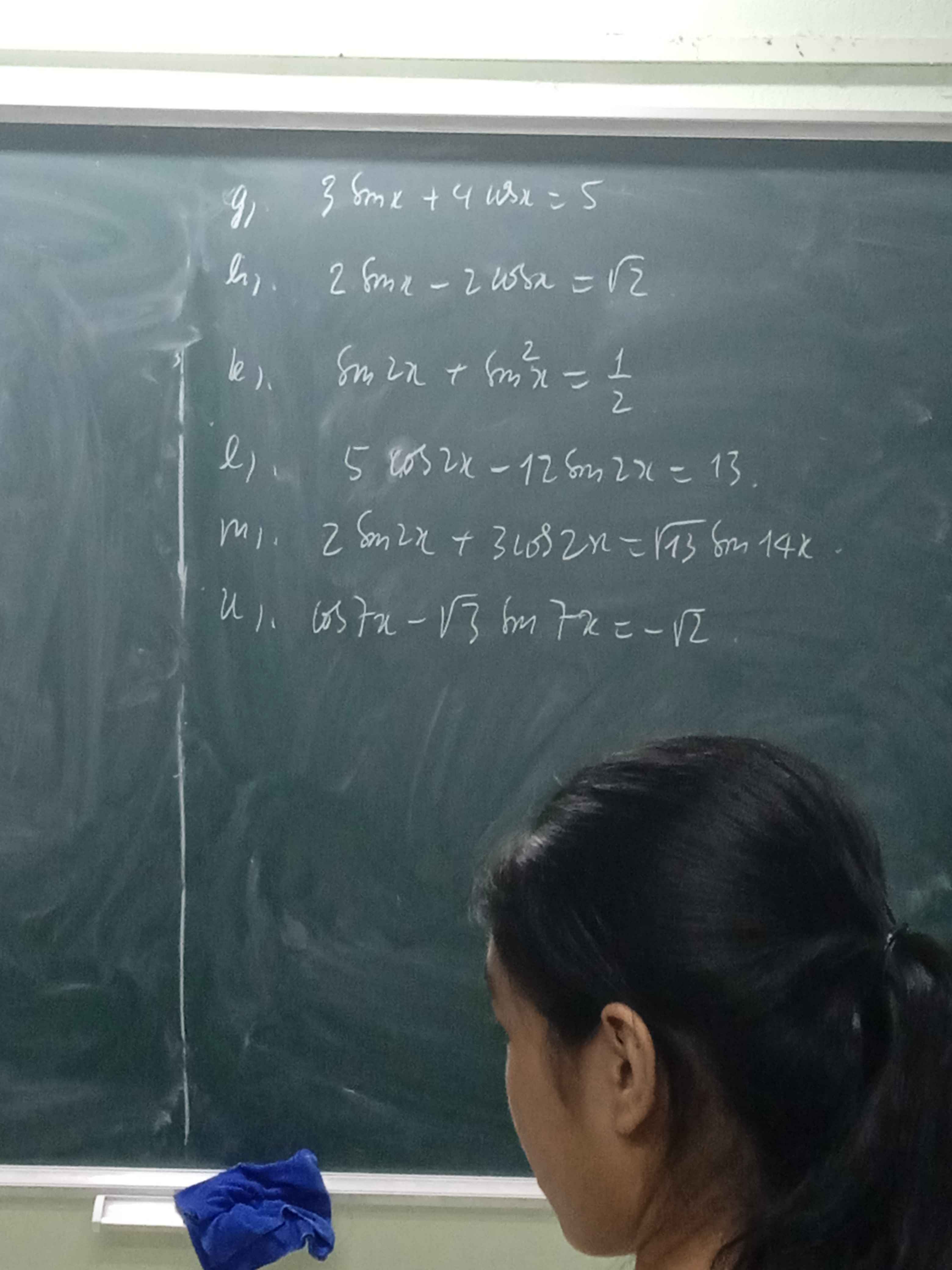g, \(3sinx+4cosx=5\)
\(\Leftrightarrow\sqrt{5}\left(\dfrac{3}{\sqrt{5}}sinx+\dfrac{4}{\sqrt{5}}cosx\right)=5\)
\(\Leftrightarrow sin\left(x+arccos\dfrac{3}{\sqrt{5}}\right)=\sqrt{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+arccos\dfrac{3}{\sqrt{5}}=arcsin\sqrt{5}+k2\pi\\x+arccos\dfrac{3}{\sqrt{5}}=\pi-arcsin\sqrt{5}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-arccos\dfrac{3}{\sqrt{5}}+arcsin\sqrt{5}+k2\pi\\x=\pi-arccos\dfrac{3}{\sqrt{5}}-arcsin\sqrt{5}+k2\pi\end{matrix}\right.\)
h, \(2sinx-2cosx=\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
k, \(sin2x+sin^2x=\dfrac{1}{2}\)
\(\Leftrightarrow1-2sin^2x+sin^2x=\dfrac{1}{2}\)
\(\Leftrightarrow sin^2x=\dfrac{1}{2}\)
\(\Leftrightarrow1-2sin^2x=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
l, \(5cos2x-12sin2x=13\)
\(\Leftrightarrow\dfrac{5}{13}cos2x-\dfrac{12}{13}sin2x=1\)
\(\Leftrightarrow cos\left(2x+arccos\dfrac{5}{13}\right)=1\)
\(\Leftrightarrow2x+arccos\dfrac{5}{13}=k2\pi\)
\(\Leftrightarrow x=-\dfrac{1}{2}arccos\dfrac{5}{13}+k\pi\)
n, \(cos7x-\sqrt{3}sin7x=-\sqrt{2}\)
\(\Leftrightarrow\dfrac{1}{2}cos7x-\dfrac{\sqrt{3}}{2}sin7x=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow cos\left(7x+\dfrac{\pi}{3}\right)=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow7x+\dfrac{\pi}{3}=\pm\dfrac{3\pi}{4}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{84}+\dfrac{k2\pi}{7}\\x=-\dfrac{13\pi}{84}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
Làm lại câu g.
\(3sinx+4cosx=5\)
\(\Leftrightarrow\dfrac{3}{5}sinx+\dfrac{4}{5}cosx=1\)
\(\Leftrightarrow sin\left(x+arccos\dfrac{3}{5}\right)=1\)
\(\Leftrightarrow x+arccos\dfrac{3}{5}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{2}-arccos\dfrac{3}{5}+k2\pi\)