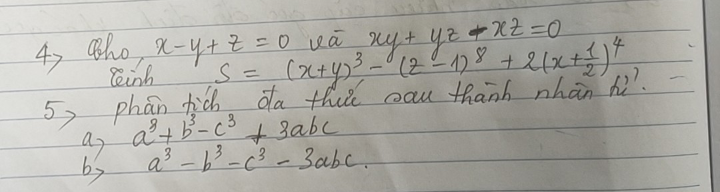4.
\(x-y+z=0\)
\(\Rightarrow\left(x-y+z\right)^2=0\)
\(\Rightarrow x^2+y^2+z^2-2xy+2xz-2yz=0\)
\(\Rightarrow x^2+y^2+z^2-2\left(xy+yz-xz\right)=0\)
\(\Rightarrow x^2+y^2+z^2=0\)
\(\Leftrightarrow x=y=z=0\)
\(S=0^3-\left(-1\right)^8+2\left(0+\dfrac{1}{2}\right)^4=\dfrac{9}{8}\)
5a.
\(a^3+b^3+3ab\left(a+b\right)-3ab\left(a+b\right)-c^3+3abc\)
\(=\left(a+b\right)^3-c^3-3ab\left(a+b-c\right)\)
\(=\left(a+b-c\right)\left(\left(a+b\right)^2+c\left(a+b\right)+c^2\right)-3ab\left(a+b-c\right)\)
\(=\left(a+b-c\right)\left(a^2+b^2+c^2-ab+bc+ac\right)\)
b. Tương tự, áp dụng kết quả phần a:
\(a^3+\left(-b\right)^3-c^3+3a\left(-b\right)c\)
\(=\left(a+\left(-b\right)-c\right)\left(a^2+\left(-b\right)^2+c^2-a\left(-b\right)+\left(-b\right)c+ac\right)\)
\(=\left(a-b-c\right)\left(a^2+b^2+c^2+ab-bc+ac\right)\)