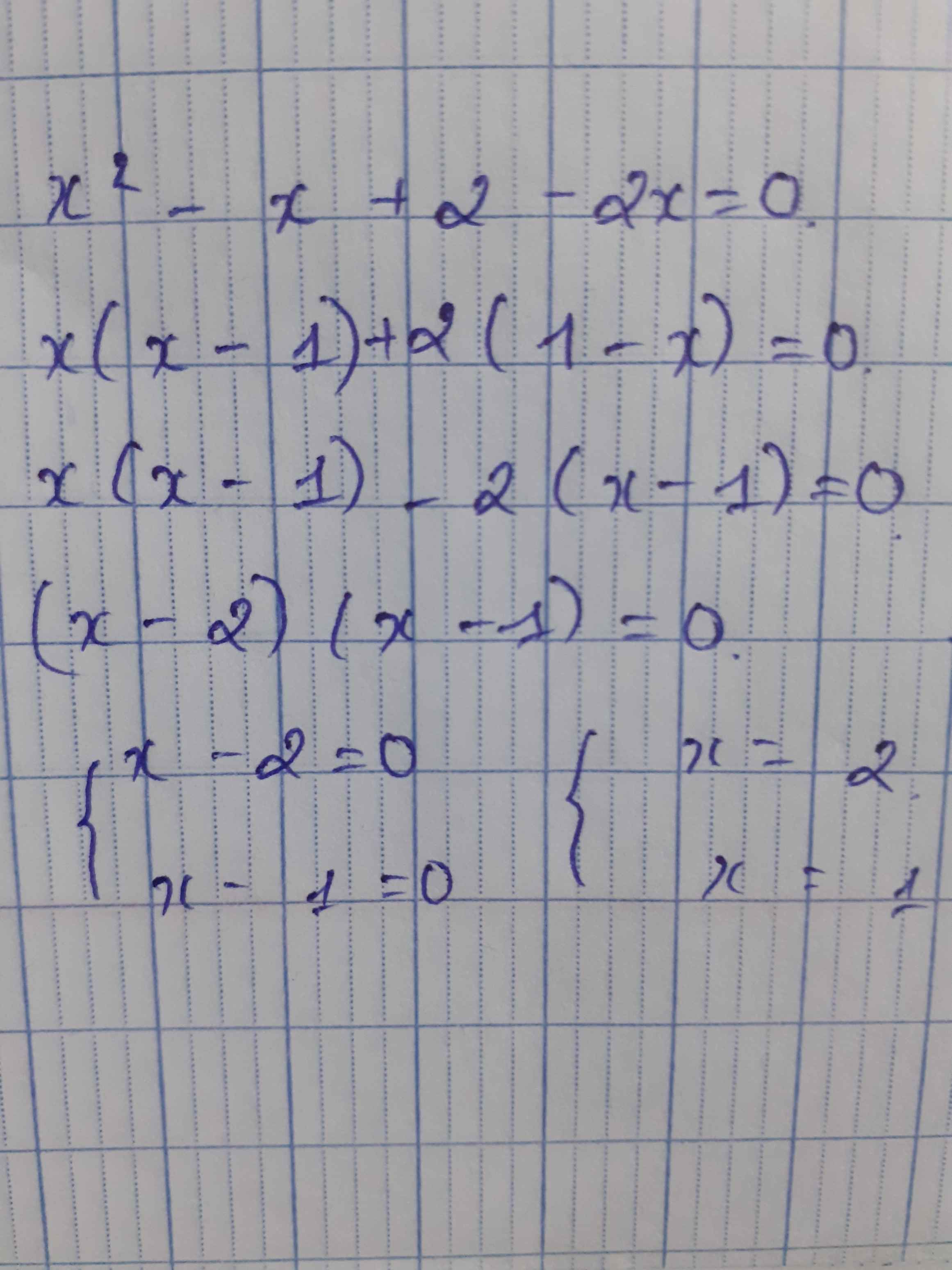\(x^2-3x+2=0\)
\(\Leftrightarrow x^2-x-2x+2=0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Vậy \(x\in\left\{1;2\right\}\)
x2 - 3x + 2 = 0
\(\Rightarrow\) x(x - 3) = - 2 = 1 . (- 2) = - 1 . 2
\(\Rightarrow\) \(\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\)
x2 - 3x + 2 = 0
\(\Leftrightarrow\) x2 - x - 2x + 2 = 0
\(\Leftrightarrow\) (x2 - x) - (2x - 2) = 0
\(\Leftrightarrow\) x ( x - 1) - 2 ( x - 1) = 0
\(\Leftrightarrow\) (x - 1) (x - 2) = 0
Khi x - 1 = 0 hoac x - 2 = 0
\(\Leftrightarrow\) x = 1 \(\Leftrightarrow\) x = 2
Vay S = \(\left\{1,2\right\}\)
Chuc ban hoc tot
Ta có: \(x^2-3x+2=0\)
a=1; b=-3; c=2
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{2}{1}=2\)
Vậy: S={1;2}