Cho hàm số \(y=f\left(x\right)\), xác định trên \(R\backslash\left\{-1;1\right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên sau :
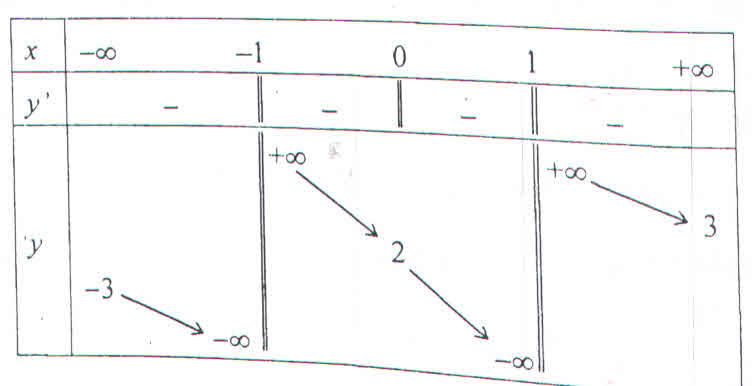
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng \(y=2m+1\) cắt đồ thị tại hai điểm phân biệt ?
- \(m\le-2\).
- \(m\ge1\).
- \(m\le-2\) hoặc \(m\ge1\).
- \(m< -2\) hoặc \(m>1\).