Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Nội dung lý thuyết
I. ĐỊNH NGHĨA
Cho hàm số \(y=f\left(x\right)\) xác định trên tập \(D\)
a) Số \(M\) được gọi là giá trị lớn nhất của hàm số \(y=f\left(x\right)\) trên tập \(D\) nếu \(f\left(x\right)\le M\) với mọi \(x\) thuộc \(D\) và tồn tại \(x_0\in D\) sao cho \(f\left(x_0\right)=M\).
Kí hiệu: \(M=\max\limits_Df\left(x\right)\)
b) Số \(m\) được gọi là giá trị nhỏ nhất của hàm số \(y=f\left(x\right)\) trên tập \(D\) nếu \(f\left(x\right)\ge m\) với mọi \(x\) thuộc \(D\) và tồn tại \(x_0\in D\) sao cho \(f\left(x_0\right)=m\).
Kí hiệu: \(m=\min\limits_Df\left(x\right)\).
Ví dụ 1: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=x-5+\dfrac{1}{x}\) trên khoảng \(\left(0;+\infty\right)\).
Giải:
Trên khoảng \(\left(0;+\infty\right)\) ta có \(y'=1-\dfrac{1}{x^2}=\dfrac{x^2-1}{x^2}\)
\(y'=0\Leftrightarrow x^2-1=0\Leftrightarrow x=1\)
Bảng biến thiên:
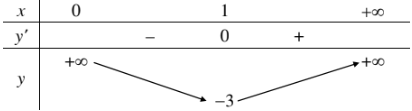
Từ bảng biến thiên ta thấy trên khoảng \(\left(0;+\infty\right)\) hàm số có giá trị cực tiểu duy nhất, đó cũng là giá trị nhỏ nhất của hàm số.
Vậy \(\min\limits_{\left(0;+\infty\right)}f\left(x\right)=-3\) (tại \(x=1\)). Không tồn tại giá trị lớn nhất của hàm số trên khoảng \(\left(0;+\infty\right)\).
@2320986@
II. CÁCH TÍNH GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ TRÊN MỘT ĐOẠN
1. Định lí
Mọi hàm số liên tục trên một đoạn đều có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn đó.
Ví dụ 2: Tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sin x\)
a) Trên đoạn \(\left[\dfrac{\pi}{6};\dfrac{7\pi}{6}\right]\) ;
b) Trên đoạn \(\left[\dfrac{\pi}{6};2\pi\right]\).
Giải:
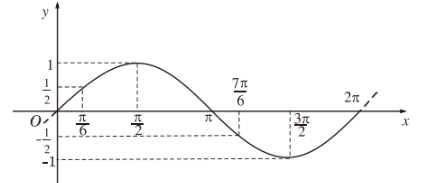
Từ đồ thị của hàm số \(y=\sin x\) ta thấy:
a) Trên đoạn \(D=\left[\dfrac{\pi}{6};\dfrac{7\pi}{6}\right]\) ta có: \(y\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2};y\left(\dfrac{\pi}{2}\right)=1;y\left(\dfrac{7\pi}{6}\right)=-\dfrac{1}{2}\)
Từ đó \(\max\limits_Dy=1\), \(\min\limits_Dy=-\dfrac{1}{2}\).
b) Trên đoạn \(E=\left[\dfrac{\pi}{6};2\pi\right]\) ta có: \(y\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2};y\left(\dfrac{\pi}{2}\right)=1;y\left(\dfrac{3\pi}{6}\right)=-1;y\left(2\pi\right)=0\)
Từ đó \(\max\limits_Ey=1\) ; \(\min\limits_Ey=-1\).
2. Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên một đoạn
Nhận xét:
Nếu đạo hàm \(f'\left(x\right)\) giữ nguyên dấu trên đoạn \(\left[a;b\right]\) thì hàm số đồng biến hoặc nghịch biến trên cả đoạn. Do đó \(f\left(x\right)\) đạt được giá trị nhỏ nhất và giá trị lớn nhất tại các đầu mút của đoạn.
Nếu chỉ có một số hữu hạn các điểm \(x_i\left(x_i< x_{i+1}\right)\) mà tại đó \(f'\left(x\right)\) bằng 0 hoặc không xác định thì hàm số \(y=f\left(x\right)\) đơn điệu trên mỗi khoảng \(\left(x_i;x_{i+1}\right)\). Rõ ràng giá trị lớn nhất (giá trị nhỏ nhất) của hàm số trên đoạn \(\left[a;b\right]\) là số lớn nhất (số nhỏ nhất) trong các giá trị của hàm số tại hai đầu mút \(a,b\) và các điểm \(x_i\) nói trên.
Quy tắc:
1. Tìm các điểm \(x_1,x_2,...,x_n\) trên khoảng \(\left(a,b\right)\) mà tại đó \(f'\left(x\right)\) bằng 0 hoặc không xác định.
2. Tính \(f\left(a\right),f\left(x_1\right),f\left(x_2\right),...,f\left(x_n\right),f\left(b\right)\).
3. Tìm số lớn nhất \(M\) và số nhỏ nhất \(m\) trong các số trên. Ta có
\(M=\max\limits_{\left[a;b\right]}f\left(x\right),m=\min\limits_{\left[a;b\right]}f\left(x\right)\)
Chú ý: Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó.
Ví dụ 3: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\dfrac{2-x}{1-x}\) trên đoạn \(\left[2;4\right]\).
Giải:
Hàm số xác định với mọi \(x\ne1\).
Ta có: \(y'=\dfrac{1}{\left(x-1\right)^2}>0,\forall x\ne1\)
Trên đoạn \(\left[2;4\right]\) ta có: \(y\left(2\right)=0;y\left(4\right)=\dfrac{2}{3}\)
Vậy \(\max\limits_{\left[2;4\right]}y=\dfrac{2}{3}\) (tại \(x=4\)) và \(\min\limits_{\left[2;4\right]}=0\) (tại \(x=2\)).
Ví dụ 4: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=x^3-3x^2-9x+35\) trên đoạn \(\left[-4;4\right]\).
Giải:
Hàm số xác định với mọi \(x\in R\).
Trên đoạn \(D=\left[-4;4\right]\). Ta có: \(y'=3x^2-6x-9\).
\(y'=0\Leftrightarrow3x^2-6x-9=0\Leftrightarrow\left[{}\begin{matrix}x=3\in D\\x=-1\in D\end{matrix}\right.\)
Ta có: \(y\left(-4\right)=-41;y\left(-1\right)=40;y\left(3\right)=8;y\left(4\right)=15\)
Vậy \(\max\limits_Dy=40\) (tại \(x=-1\)) và \(\min\limits_Dy=-41\) (tại \(x=-4\)).
@2320603@@2320368@