Bài 4: Đường tiệm cận

I. ĐƯỜNG TIỆM CẬN NGANG

Định nghĩa:

Cho hàm số \(y=f\left(x\right)\) xác định trên một khoảng vô hạn (là khoảng dạng \(\left(a;+\infty\right)\), \(\left(-\infty;b\right)\) hoặc \(\left(-\infty;+\infty\right)\)). Đường thẳng \(y=y_0\) là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số \(y=f\left(x\right)\) nếu ít nhất một trong các điều kiện sau được thoả mãn

          \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=y_0\)  ;  \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=y_0\).

Chú ý: Nếu \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}f\left(x\right)=a\), ta viết chung là \(\lim\limits_{x\rightarrow\pm\infty}f\left(x\right)=a\) (\(a\in R\)).

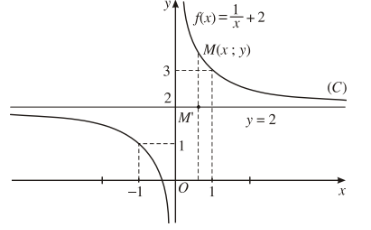
Ví dụ 1: Cho hàm số \(f\left(x\right)=\dfrac{1}{x}+2\). Xác định đường tiệm cận ngang của đồ thị hàm số.

Giải:

Hàm số xác định với mọi \(x\ne0\).

Ta có: \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{1}{x}+2\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{1}{x}+\lim\limits_{x\rightarrow+\infty}2=2\)

Tương tự \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=2\).

Vậy đường tiệm cận ngang của đồ thị hàm số trên là đường thẳng \(y=2\).

Ví dụ 2: Cho hàm số \(y=\dfrac{1}{\sqrt{x}}+1\) xác định trên khoảng \(\left(0;+\infty\right)\).

Đồ thị hàm số có tiệm cận ngang là đường \(y=1\) vì \(\lim\limits_{x\rightarrow+\infty}=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{1}{\sqrt{x}}+1\right)=1\).

II. ĐƯỜNG TIỆM CẬN ĐỨNG

Định nghĩa:

Đường thẳng \(x=x_0\) được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số \(y=f\left(x\right)\) nếu ít nhất một trong các điều kiện sau được thoả mãn

          \(\lim\limits_{x\rightarrow x_0^+}f\left(x\right)=+\infty\)   ;  \(\lim\limits_{x\rightarrow x_0^-}f\left(x\right)=-\infty\)  ;

          \(\lim\limits_{x\rightarrow x_0^+}f\left(x\right)=-\infty\)   ;   \(\lim\limits_{x\rightarrow x_0^-}f\left(x\right)=+\infty\).

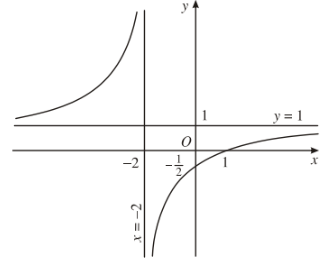
Ví dụ 3: Tìm các đường tiệm cận đứng và ngang của đồ thị hàm số \(y=\dfrac{x-1}{x+2}\) (C).

Giải:

Vì \(\lim\limits_{x\rightarrow-2^+}\dfrac{x-1}{x+2}=-\infty\) (hoặc \(\lim\limits_{x\rightarrow-2^-}\dfrac{x-1}{x+2}=+\infty\)) nên đường thẳng \(x=-2\) là tiệm cận đứng của (C).

Vì \(\lim\limits_{x\rightarrow\pm\infty}\dfrac{x-1}{x+2}=1\) nên đường thẳng \(y=1\) là tiệm cận ngang của (C). 

Ví dụ 4: Tìm tiệm cận  đứng của đồ thị hàm số \(y=\dfrac{2x^2+x+1}{2x-3}\).

Giải:

Vì \(\lim\limits_{x\rightarrow\left(\dfrac{3}{2}\right)^+}\dfrac{2x^2+x+1}{2x-3}=+\infty\) (hoặc \(\lim\limits_{x\rightarrow\left(\dfrac{3}{2}\right)^-}\dfrac{2x^2+x+1}{2x-3}=-\infty\)) nên đường thẳng \(x=\dfrac{3}{2}\) là tiệm cận đứng của đồ thị hàm số đã  cho.