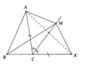
Trên tia đối của tia CB lấy điểm A' sao cho CA' = CA. Sử dụng tính chất của tam giác cân ta có được CM là đường trung trực của AA' Þ MA = MA'. Sử dụng bất đẳng thức trong tam giác A'MB ta có: CA + CB = CA' + CB = BA' <MA' + MB Þ CA + CB < MA + MB.
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C (M khác C). Chứng minh rằng AC+ CB < AM+ MB
Cho tam giác ABC . Điểm M nằm trên đường phân giác của góc ngoài đỉnh C( M khác C ) . Chứng minh AC + CB < AM +MB .
cho tam giác ABC .Điểm M nằm trên đường phân giác của góc ngoài đỉnh C (M khác C ).Chứng minh rằng AC+CB<AM+MB
Mấy bạn giải giúp mik bài này với :
Cho tam giác ABC . Điểm M nằm trên đường phân giác của góc ngoài đỉnh C ( M khác C ). Chứng minh rằng AC + CB < AM + MB
Cho tam giác ABC . Điểm N nằm trên đường phân giác của góc ngoài đỉnh C (M # C )
c/m AC+CB< AM+BM
Cho tam giác ABC nhọn ( AB < AC ). Điểm M nằm trên đường phân giác của góc ngoài đỉnh C ( M khác C ). Chứng minh rằng AC + BC < AM + BM.
cho tam giác ABC m nằm trên phân giác ngoài góc C chứng minh MA+mb lớn hơn hoặc bằng CA+CB
cho tam giac ABC. điểm M nằm trên đường phân giác ngoài của góc C (M khác C). CMR CA+ CB <MA+MB
Cho tam giác abc ko cân tại a, có phân giác góc ngoài tại đỉnh a cắt đường thẳng bc tại điểm m. Khi đó ta có:
A. MB/MC=AM/AC
B. MB/MC=AC/AB
C. MC/MB=AC/AB
D. MC/MB=AC/AB
