Các câu hỏi tương tự
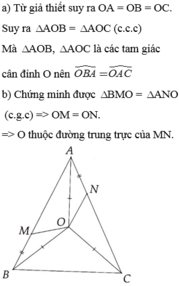
Cho tam giác ABC cân tại A Gọi D là điểm cách đều 3 đỉnh. Nối OA,OB,OC với nhau. Chứng minh
a) góc OBA = góc OAC
b) trên AB lấy M trên AC lấy N sao cho BM = AN. Chứng minh: O thộc Đường trung trực của MN
cho tam giác ABC, trên cạnh AB lấy M, trên cạnh AC lấy N sao cho BM=CN. Gọi O là trung điểm của MN. Trên tia đối của tia OB lấy điểm I sao cho O là trung điểm của BI. Chứng minh rằng:
a, BM // NI
b, tam giác NIC cân
c,góc BAC= 2 góc NCI
Cho tâm giác ABC, trên cạnh AB lấy M, trên cạnh AC lấy N sao cho BM=CN. Gọi O là trung điểm của MN. Trên tia đối của tia OB lấy điểm I sao cho O là trung điểm của BI. Chứng minh rằng:
a) BM // NI
b) Tam giác NIC cân
c) Góc BAC = 2 lần góc NCI
Bài 1: Cho tam giác ABC cân (ABAC), O là giao điểm 3 trung trực 2 cạnh của tam giác ABC (O nằm trong tam giác). Trên tia đối của các tia AB và CA ta lấy 2 điểm M, N sao cho AMCN. Chứng minh:a) Góc OAB góc OCAb) Tam giác AOM tam giác CONc) Hai trung trực OM, ON cắt nhau tại I. Chứng minh OI là tia phân giác của góc MONBài 2: Cho góc nhọn xOy; trên tia Ox lấy 2 điểm A và B (A nằm giữa O, B). Trên Oy lấy 2 điểm C, D (C nằm giữa O, D) sao cho OAOC và OBOD. Chứng minh:a) Tam giác AOD tam giác COBb...
Đọc tiếp
Bài 1: Cho tam giác ABC cân (AB=AC), O là giao điểm 3 trung trực 2 cạnh của tam giác ABC (O nằm trong tam giác). Trên tia đối của các tia AB và CA ta lấy 2 điểm M, N sao cho AM=CN. Chứng minh:
a) Góc OAB = góc OCA
b) Tam giác AOM = tam giác CON
c) Hai trung trực OM, ON cắt nhau tại I. Chứng minh OI là tia phân giác của góc MON
Bài 2: Cho góc nhọn xOy; trên tia Ox lấy 2 điểm A và B (A nằm giữa O, B). Trên Oy lấy 2 điểm C, D (C nằm giữa O, D) sao cho OA=OC và OB=OD. Chứng minh:
a) Tam giác AOD = tam giác COB
b) Tam giác ABD = tam giác CDB
c) Gọi I là giao điểm của AD và BC. Chứng minh IA=IC; IB=ID
Bài 3: Cho tam giác ABC. Qua A kẻ đường thẳng song song với BC, qua C kẻ đường thẳng song song với AB, hai đường thẳng này cắt nhau tại D
a) Chứng minh: AD=BC và AB=DC
b) Gọi M, N lần lượt là trung điểm của BC và AD. Chứng minh: AM=CN
c) Gọi O là giao điểm của AC và BD. Chứng minh: OA=OC và OB=OD
d) Chứng minh: M, O, N thẳng hàng
Bài 4: Cho góc xOy = 60 độ. Vẽ Oz là tia phân giác của góc xOy
a) Tính góc xOy?
b) Trên Ox lấy điểm A và trên Oy lấy điểm B sao cho OA=OB. Tia Oz cắt AB tại I. Chứng minh tam giác OIA = tam giác OIB
c) Chứng minh OI vuông góc AB
d) Trên tia Oz lấy điểm M. Chứng minh MA=MB
e) Qua M vẽ đường thẳng song song với AB cắt tia Ox, Oy lần lượt tại C và D. Chứng minh BD=AC
Mọi ng giúp mình giải bài này nhé! Cảm ơn mn <3
Cho tam giác MNP cân tại M. Trên cạnh MN lấy điểm K, trên cạnh MP lấy điểm D sao cho MK DP. Đường trung trực của MP cắt đường trung trực của DK tại O. Chứng minh:a)
M
K
O
^
P
D
O
^
;b) O thuộc đường trung trực của MN;c) MO là tia phân giác của
N
M
P...
Đọc tiếp
Cho tam giác MNP cân tại M. Trên cạnh MN lấy điểm K, trên cạnh MP lấy điểm D sao cho MK = DP. Đường trung trực của MP cắt đường trung trực của DK tại O. Chứng minh:
a) M K O ^ = P D O ^ ;
b) O thuộc đường trung trực của MN;
c) MO là tia phân giác của N M P ^ .
Mn giúp mk bài này vs ạBài toán 1: Cho tam giác ABC cân tại A, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm 0 cách đều 3 đỉnh của tam giác ABC. Bài toán 2: Cho tam giác cân ABC (AB AC). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của góc ACB. Tính các góc của tam giác ABC.Bài toán 3: Cho tam giác đều ABC. Trên các cạnh AB, BC, CA lấy theo thứ tự ba điểm M, N, P sao cho AM BN CP.a) Chứng minh tam giác MNP là tam giác đều b) Gọi O là giao điểm các đư...
Đọc tiếp
Mn giúp mk bài này vs ạ
Bài toán 1: Cho tam giác ABC cân tại A, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm 0 cách đều 3 đỉnh của tam giác ABC.
Bài toán 2: Cho tam giác cân ABC (AB = AC). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của góc ACB. Tính các góc của tam giác ABC.
Bài toán 3: Cho tam giác đều ABC. Trên các cạnh AB, BC, CA lấy theo thứ tự ba điểm M, N, P sao cho AM = BN = CP.
a) Chứng minh tam giác MNP là tam giác đều b) Gọi O là giao điểm các đường trung trực của tam giác ABC. Chứng minh rằng 0 cũng là
giao điểm của các đường trung trực của tam giác MNP.
Cho tam giác ABC ( AB = AC > BC) . Trên AB và AC lấy 2 điểm M và N sao cho BM= AN. Gọi o là điểm cách điều 3 đỉnh A; B; C của tam giác ABC
a) Chứng miinh góc ABO = góc CAO
b) Chứng minh: O cách đều hai điểm M và N
Cho tam giác ABC cân tại A. Trên các cạnh AC,AB lần lượt lấy M, N sao cho AM = AN.
a) Chứng minh A B M ^ = A C N ^
b) Gọi O là giao điểm của BM và CN. Chứng minh tam giác OBC cân.
Trên ba cạnh AB, BC và CA của tam giác đều ABC lấy các điểm theo thứ tự M, N, P sao cho AM BN CP. Gọi O là giao điểm ba đường trung trực của tam giác ABC.a) Tính số đo góc
M
A
O
^
.b) Chứng minh
∆
M
A
O
∆
O
P
C
.
c) Chứng minh O là giao điểm ba đường trung trực của tam giác MNP.
Đọc tiếp
Trên ba cạnh AB, BC và CA của tam giác đều ABC lấy các điểm theo thứ tự M, N, P sao cho AM = BN = CP. Gọi O là giao điểm ba đường trung trực của tam giác ABC.
a) Tính số đo góc M A O ^ .
b) Chứng minh ∆ M A O = ∆ O P C .
c) Chứng minh O là giao điểm ba đường trung trực của tam giác MNP.