Gọi vận tốc ô tô dự định là v (km/h), (v > 6)
Thời gian đi nửa quãng đường đầu là 30/(v+10) (h)
Thời gian đi nửa quãng đường sau là 30/(v-6) (h)
Thời gian dự định đi quãng đường AB là 60/v (h)
Theo bài ra ta có:
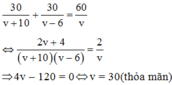
Vậy thời gian dự định là 60/30 = 2 giờ
Đáp án: B











