1) Cho don thuc 12x5y2 ( -12,5zx2y5z)
a) Hay thu gon don thuc va xac dinh bac cua don thuc thu gon
b) Viet don thuc thu gon tren thanh tong cua 2 don thuc
Ôn tập chương V
a) Ta có: \(12x^5y^2\cdot\left(-12.5zx^2y^5z\right)\)
\(=\left(-12.5\cdot12\right)\cdot\left(x^5\cdot x^2\right)\cdot\left(y^2\cdot y^5\right)\cdot z^2\)
\(=-150x^7y^7z^2\)
Đúng 0
Bình luận (0)
1) Cho △ABC can o A. Tren tia doi cua cac tia BC va CB lay thu tu hai diem F va E sao cho BF = CE
a) Chung minh: △AEF can
b) Goi M la trung diem cua BC. Chung minh AM la tia phan giac goc FAE
c) Tu B va C ke BH, CK theo thu tu vuong goc voi AF va AE ( H ∈ AF, K ∈ AE ). Chung minh BH = CK
Đăng vào phần lớp 8 ấy, thế này kh ai giải cho đâu.
Đúng 0
Bình luận (0)
a) Ta có: \(\widehat{ABF}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔBAC cân tại A)
nên \(\widehat{ABF}=\widehat{ACE}\)
Xét ΔABF và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{ABF}=\widehat{ACE}\)(cmt)
BF=CE(gt)
Do đó: ΔABF=ΔACE(c-g-c)
Suy ra: AF=AE(Hai cạnh tương ứng)
Xét ΔAFE có AF=AE(Cmt)
nên ΔAFE cân tại A(Định nghĩa tam giác cân)
Đúng 0
Bình luận (0)
1) Dieu tra ve diem kiem tra toan 15 phut cua 30 hoc sinh giao vien ghi lai bang 1 nhu sau:48691067758573461035696466768775 a) Dau hieu la gi? Co bao nhieu gia tri khac nhaub) Lap bang tan so, tinh so trung binh cong, Tim mot cua dau hieu
Đọc tiếp
1) Dieu tra ve diem kiem tra toan 15 phut cua 30 hoc sinh giao vien ghi lai bang 1 nhu sau:
| 4 | 8 | 6 | 9 | 10 | 6 | 7 | 7 | 5 | 8 |
| 5 | 7 | 3 | 4 | 6 | 10 | 3 | 5 | 6 | 9 |
| 6 | 4 | 6 | 6 | 7 | 6 | 8 | 7 | 7 | 5 |
a) Dau hieu la gi? Co bao nhieu gia tri khac nhau
b) Lap bang tan so, tinh so trung binh cong, Tim mot cua dau hieu
a) Dấu hiệu là điểm kiểm tra 15 phút toán của 30 bạn học sinh
Ở đây có 8 giá trị khác nhau
Đúng 0
Bình luận (0)
lop 10 cung co thong ke nma day la bai lop 7 ban a :((
Đúng 0
Bình luận (0)
1) Cho don thuc 2x2y ( -2,5x3y2z)
a) Hay thu gon don thuc va xac dinh bac cua don thuc thu gon
b) Viet don thuc thu gon tren thanh tong cua 2 don thuc
a) Ta có: \(2x^2y\cdot\left(-2.5x^3y^2z\right)\)
\(=\left(-2.5\cdot2\right)\cdot\left(x^2\cdot x^3\right)\cdot\left(y\cdot y^3\right)\cdot z\)
\(=-5x^5y^4z\)
Đúng 0
Bình luận (0)
1) Giai phuong trinh 2ab = 0
\(2ab=0\Leftrightarrow\left[{}\begin{matrix}a=0\\b=0\end{matrix}\right.\)
Đã bảo bạn là đăng vào phần lớp 8 ấy. Sẽ có những người học cùng cấp giải cho bạn.
Đúng 2
Bình luận (0)
Ta có: 2ab=0
nên \(\left\{{}\begin{matrix}a=0\\b=0\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Tan alpha - 2 pi < alpha < 3pi/2
CM: cos (a+b) cos( a-b)= cos^2a - sin^2 b = cos^2- sin^a
\(cos\left(a+b\right)cos\left(a-b\right)=\dfrac{1}{2}cos\left(a+b+a-b\right)+\dfrac{1}{2}cos\left(a+b-a+b\right)\)
\(=\dfrac{1}{2}cos2a+\dfrac{1}{2}cos2b\)
\(=\dfrac{1}{2}\left(2cos^2a-1\right)+\dfrac{1}{2}\left(1-2sin^2b\right)\)
\(=cos^2a-sin^2b\)
Đúng 1
Bình luận (0)
ĐKXĐ: \(\left(4x-6\right)\left(9-3x\right)\ge0\)
\(\Leftrightarrow\left(x-\dfrac{3}{2}\right)\left(3-x\right)\ge0\)
\(\Rightarrow\dfrac{3}{2}\le x\le3\)
Hay \(D=\left[\dfrac{3}{2};3\right]\)
Đúng 0
Bình luận (0)
Hàm số xác định `<=> (4x-6)(9-3x)>=0`
`<=>` \(\left[{}\begin{matrix}\left\{{}\begin{matrix}4x-6\ge0\\9-3x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}4x-6\le0\\9-3x\le0\end{matrix}\right.\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x\le3\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{3}{2}\\x\ge3\end{matrix}\right.\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}\dfrac{3}{2}\le x\le3\\VN\end{matrix}\right.\)
Vậy `S=[3/2 ; 3]`.
Đúng 0
Bình luận (0)
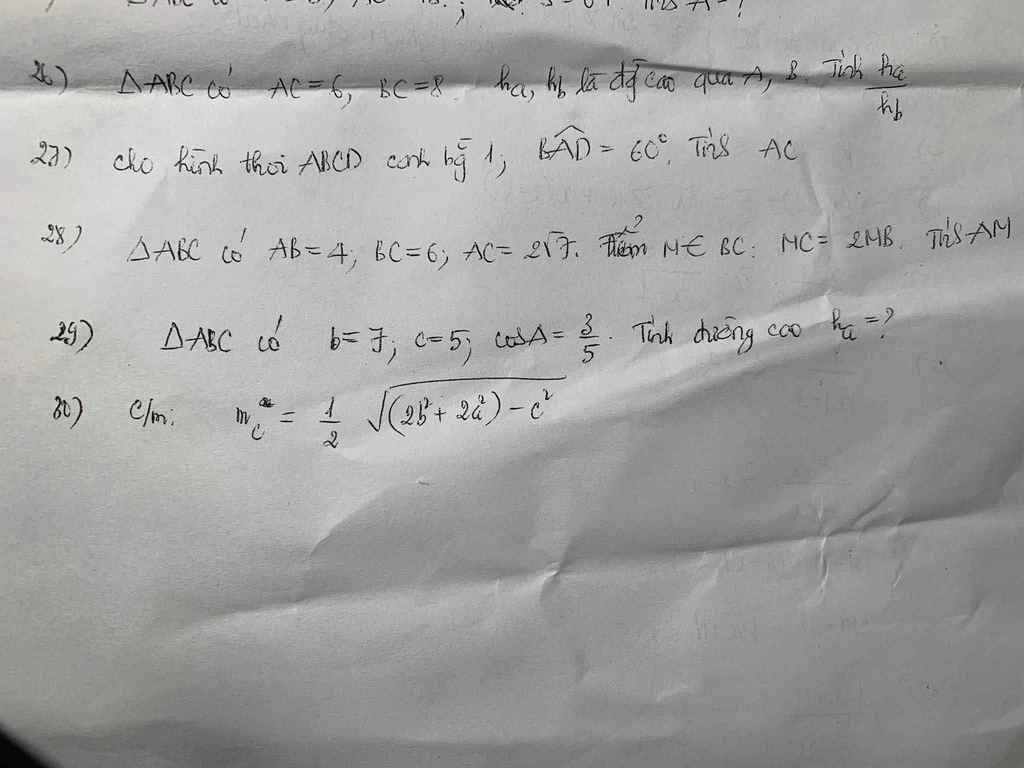
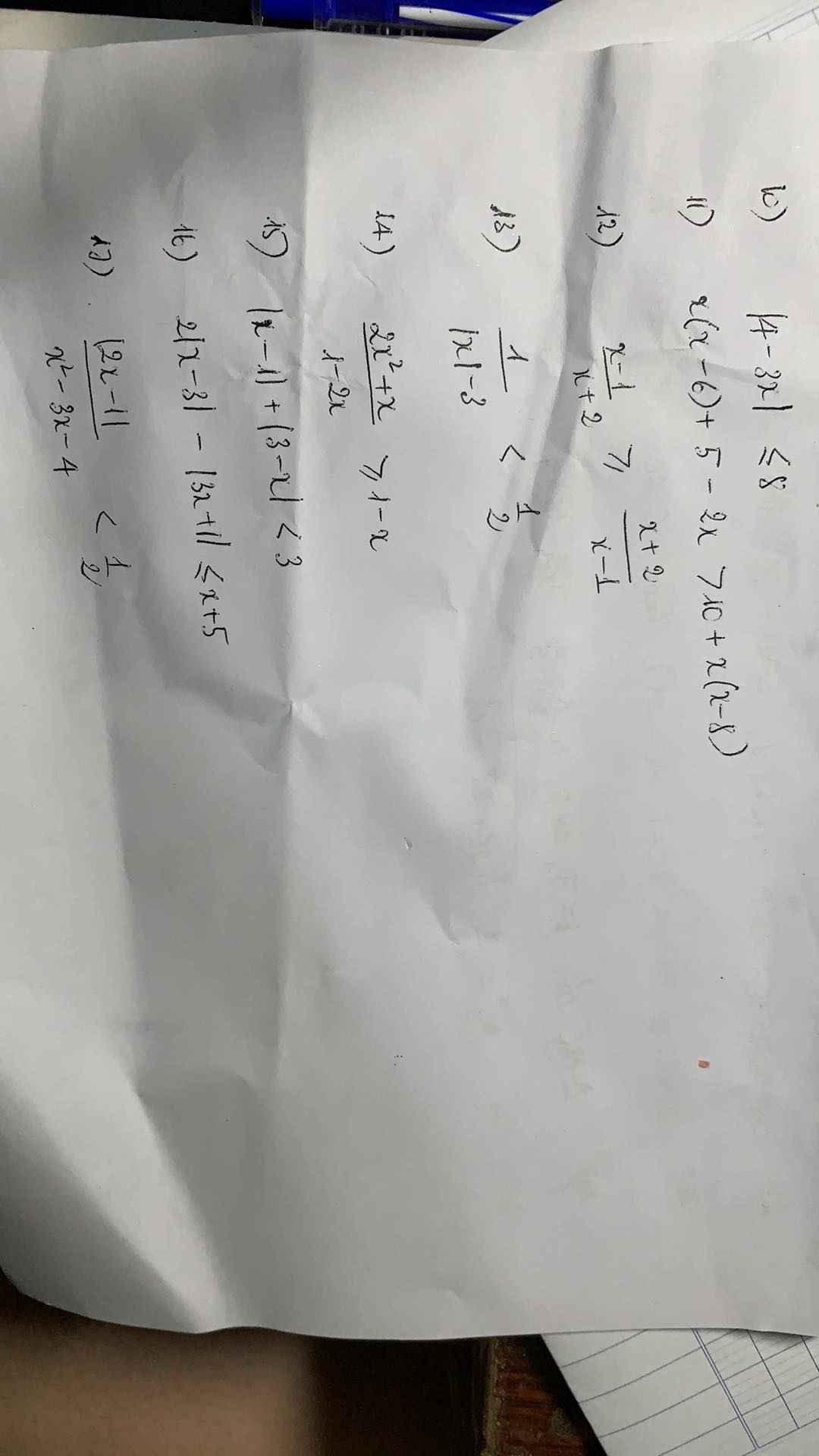
giúp mình với ạ
