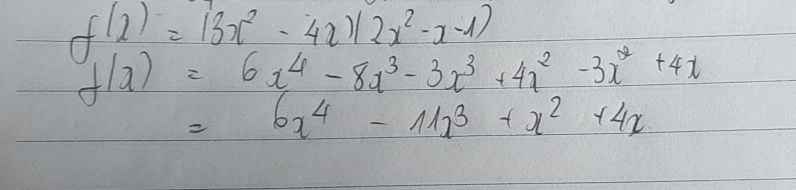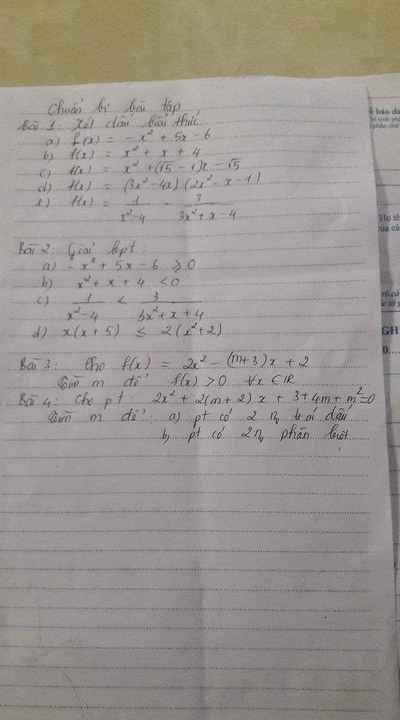
Ôn tập chương V

câu a

Giả sử \(C\)  cần tìm có tọa độ là \(\left(x;y\right)\). Để tam giác ABC vuông cân tại B ta phải có:

\(\left\{{}\begin{matrix}\overrightarrow{BA}.\overrightarrow{BC}=0\\\left|\overrightarrow{BA}\right|=\left|\overrightarrow{BC}\right|\end{matrix}\right.\)  với \(\overrightarrow{BA}=\left(1;3\right)\)  và \(\overrightarrow{BC}=\left(x-1;y-1\right)\)

Điều đó có nghĩa là:

\(\left\{{}\begin{matrix}1.\left(x-1\right)+3\left(y-1\right)=0\\1^2+3^2=\left(x-1\right)^2+\left(y-1\right)^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=4-3y\\\left(3-3y\right)^2+\left(y-1\right)^2=10\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=4-3y\\10y^2-20y=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=2\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}C\left(4;0\right)\\C\left(-2;2\right)\end{matrix}\right.\)

Có \(C_{10}^2\) cách chọn 2 nhóm bất kì (không gian mẫu)

Có 2 biến cố thuận lợi: 1,2 hoặc 3,4

Do đó xác suất là: \(P=\dfrac{2}{C_{10}^2}\)

Số chia hết cho 4 khi 2 chữ số tận cùng của nó chia hết cho 4, nên ý tưởng ở đây là chọn 2 số tận cùng trước.

Có \(\dfrac{96-04}{4}+1=24\) số có 2 chữ số chia hết cho 4 (tính cả những số bắt đầu bằng 0 như 04, 08...)

Loại ra 2 trường hợp 2 chữ số trùng nhau là \(44\) và \(88\), ta còn 22 chữ số.

Chia 22 chữ số này làm 2 loại: có chứa chữ số 0 bao gồm 6 số là 04, 08, 20, 40, 60, 80 và 16 số không chứa chữ số 0

- TH1: 2 chữ số cuối có chứa 0, chọn 3 chữ số còn lại từ 8 chữ số còn lại và hoán vị chúng có \(A_8^3\) cách \(\Rightarrow6.A_8^3\) số

- TH2: 2 chữ số cuối không chứa chữ số 0:

+ Chọn 3 chữ số còn lại 1 cách bất kì và hoán vị: \(A_8^3\) cách

+ Chọn 3 chữ số còn lại có mặt chữ số 0 và hoán vị sao cho số 0 đứng đầu: \(A_7^2\) cách

\(\Rightarrow16.\left(A_8^3-A_7^2\right)\) số

Cộng 2 trường hợp lại