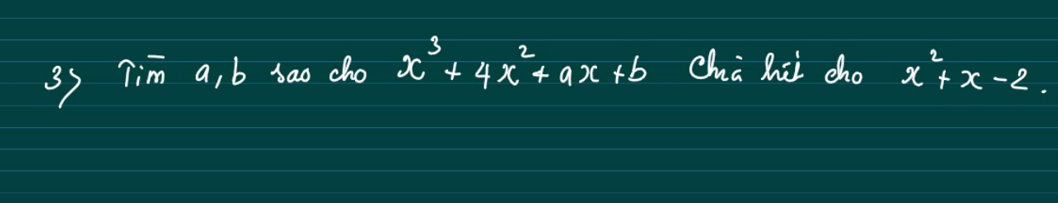Bài 8: Phép chia các phân thức đại số

Bài 2: 

a: \(\dfrac{x^2+2x+1}{x+1}=x+1\)

b: \(\dfrac{x^3+8}{x+2}=x^2-2x+4\)

c: \(\dfrac{x^3+3x^2+3x+1}{x+1}=x^2+2x+1\)

d: \(\dfrac{a^2-6ab+9b^2}{a-3b}=a-3b\)

a: ĐKXĐ: \(x\ne-1\)

b: \(B=\dfrac{5}{x+1}+\dfrac{10}{x^2-x+1}-\dfrac{15}{x^3-1}\)

\(=\dfrac{5x^2-5x+5+10x+10-15}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{5x^2+5x}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{5x}{x^2-x+1}\)

\(x^3+4x^2+ax+b=x\left(x^2+x-2\right)+3\left(x^2+x-2\right)-x+ax+6+b\)

\(=\left(x^2+x+2\right)\left(x+2\right)-x+ax+6+b⋮\left(x^2+x+2\right)\)

\(\Rightarrow-x+ax+6+b=0\)

\(\Rightarrow\left\{{}\begin{matrix}ax=x\\b=-6\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-6\end{matrix}\right.\)

Để \(f\left(x\right)⋮g\left(x\right)\Leftrightarrow2x^3+3x^2-2x-a=\left(x-1\right)\cdot a\left(x\right)\)

Thay \(x=1\Leftrightarrow2+3-2-a=0\Leftrightarrow a=3\)

giúp mik với ạ , mai nộp rồi

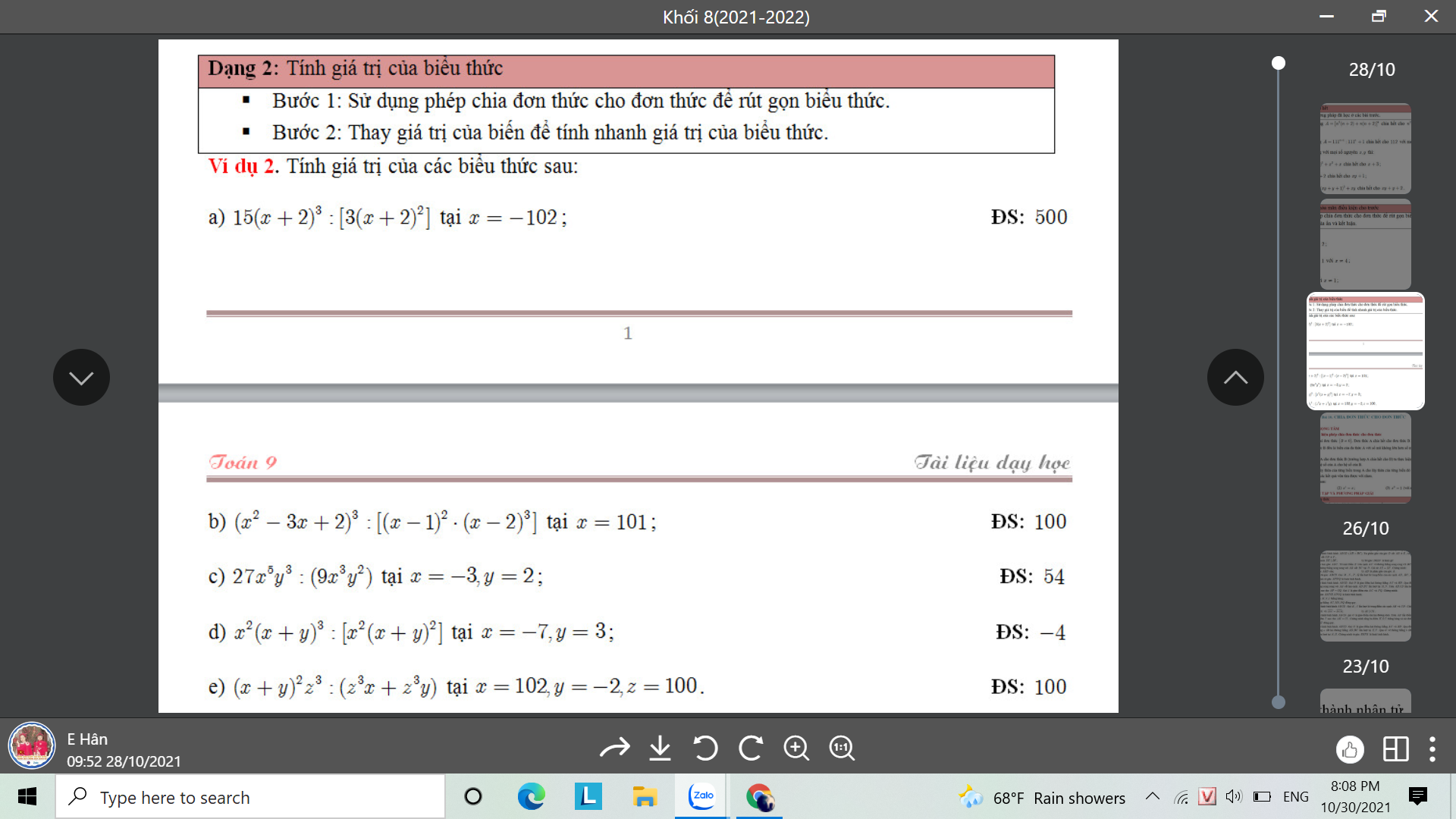
c: \(\dfrac{27x^5y^3}{9x^3y^2}=3x^2y\)

\(=3\left(-3\right)^2\cdot2=3\cdot9\cdot2=54\)

\(a,=\dfrac{1-2x+x^2}{x\left(x+1\right)}:\dfrac{1+x^2-2x}{x}=\dfrac{\left(x-1\right)^2}{x\left(x+1\right)}\cdot\dfrac{x}{\left(x-1\right)^2}=\dfrac{1}{x+1}\\ b,=\dfrac{9x^2+3x+2x-6x^2}{\left(1-3x\right)\left(3x+1\right)}\cdot\dfrac{\left(1-3x\right)^2}{2x\left(3x+5\right)}\\ =\dfrac{x\left(3x+5\right)}{2x\left(3x+5\right)\left(3x+1\right)}=\dfrac{1}{2\left(3x+1\right)}\\ c,=\dfrac{9+x^2-3x}{x\left(x-3\right)\left(x+3\right)}:\dfrac{3x-9-x^2}{3x\left(x+3\right)}=\dfrac{x^2-3x+9}{x\left(x-3\right)\left(x+3\right)}\cdot\dfrac{3x\left(x+3\right)}{-\left(x^2-3x+9\right)}=\dfrac{-3}{x-3}\\ d,=\dfrac{x+1}{x+2}:\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x+3\right)^2}=\dfrac{\left(x+3\right)^2}{\left(x+2\right)^2}\)

b: \(=9x^2+3x+1\)

\(=\dfrac{-3\left(x-1\right)}{\left(1+x\right)^2}\cdot\dfrac{x+1}{6\left(x-1\right)\left(x+1\right)}\left(x\ne\pm1\right)\\ =\dfrac{-1}{2\left(x+1\right)^2}\)

\(=x^2\left(x-6\right)-24\left(x-6\right)=\left(x^2-24\right)\left(x-6\right)\)

\(x^3-6x^2-24x+144=\left(x^3-6x^2\right)-\left(24x-144\right)=x^2\left(x-6\right)-24\left(x-6\right)=\left(x-6\right)\left(x^2-24\right)\)