hãy tìm những chữ cái in hoa có tâm đối xứng. Và vẽ tâm dối xứng của các chữ cái in hoa đó
help meeeeeeeeeeeeeeeee 
Các chữ in hoa có tâm đối xứng là H,N,O,I
Cho hình 44, trong đó MD // AB và ME // AC, còn I trung điểm của ED. CMR:
a) hai tam giác EAD và DME =nhau.
b) Hai tam giác AID vá MIE =nhau.
c) Điểm A đối xứng với M qua điểm I
Vì MD//AB =>góc AEI=góc IDM (1)
EI=ID (I là TĐ ED) (2)
góc EIA = góc MID (đối đỉnh) (3)
Từ (1),(2),(3) =>Δ EAD=Δ DME =>DM=AE
Xét 2 Δ EAD và Δ DME:
cạnh ED chung (*)
DM=AE(**)
góc AED=góc EDM (so le trong) (***)
Từ(*),(**),(***)=> Δ EAD=Δ DME
Vẽ tam giác ABC :
a) vẽ các điểm M, N tương ứng là đối xứng qua điểm A của các điểm B và C
b) 2 tam giác ABC và AMN có bằng nhau k? Vì sao?
Trong các hình vẽ sau, hình nào có tâm đối xứng ?
a) Đoạn thẳng AB (h.83a);
b) Tam giác đếu ABC (h.83b);
c) Biển cấm đi ngược chiều (h.83c);
d) Biển chỉ hướng đi vòng tránh chướng ngại vật (h.83d)
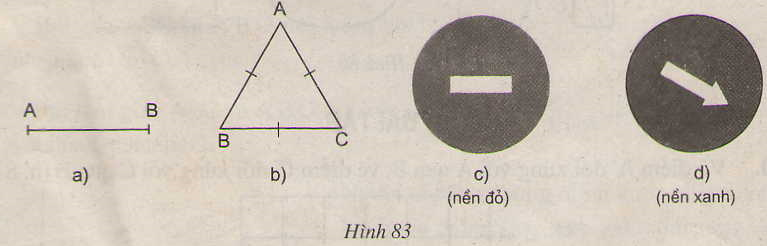
Hình 83a, c có tâm đối xứng.
Hình 83a có tâm đối xứng là trung điểm của đoạn thẳng AB,
Hình 83c có tâm đối xứng là tâm của đường tròn.
Cho hình bình hành ABCD có O là giao điểm 2 đường chéo , E là 1 điểm bất kì giữa A và B, F là điểm đối xứng E qua O.
C/M: 3 điểm D,E,C thẳng hàng
Xét tứ giác AECF có
O là trug điểm của AC
O là trung điểm của EF
Do đó: AECF là hình bình hành
Suy ra: AE//CF
=>CF//AB
mà CD//AB
và CD,CF có điểm chung là C
nên C,D,F thẳng hàng
Cho hình 44,trong đó MD//AB và ME// AC, còn I là trung điểm của ED. Chứng minh rằng:
a)Hai tam giác EAD và DME bằng nhau;
b)Hai tam giác AID và MIE bằng nhau;
c)Điểm A đối xứng với điểm M qua điểm I.
Này các bạn trong sgk trang 112 nhé!😀😄😄😆😅😂😂
Cho tam giác ABC vuông tại A, đường cao AH. gọi E là trung điểm AD và G là điểm đối xứng của C qua A. Chứng minh BE vuông góc với DG
Cho hbh ABCD. Trên các cạnh AB,BC,CD,DA lấy các điểm E,F,G,H sao cho AE=CG, BF=DH
a, Xác định tâm đối xứng của hbh ABCD
b, Cm: tứ giác EFGH là hbh và tìm tâm đối xứng của nó
c, O còn là tâm đối xứng của hbh nào nữa
a: Ta co: ABCD là hình bình hành
nên Hai đường chéo AC và DB cắt nhau tại trung điểm của mỗi đường
hay O là tâm đối xứng của hình bình hành ABCD
b: Xét tứ giác AECG có
AE//CG
AE=CG
Do đó: AECG là hình bình hành
Suy ra: AC cắt EG tại trung điểm của mỗi đường
hay O là trung điểm của EG
Xét tứ giác BHDF có
BF//DH
BF=DH
DO đó: BHDF là hình bình hành
Suy ra: Hai đường chéo BD và HF cắt nhau tại trung điểm của mỗi đường
hay O là trung điểm của HF
Xét tứ giác EHGF có
O là trung điểm của EG
O là trung điểm của HF
Do đó: EHGF là hình bình hành
Cho tam giác ABC trực tâm H,goi I là giao điểm các đường trung trực,gọi H’ đối xứng với H qua trung điểm của BC
CMR: H’ đối xứng với A qua I
Lời giải:
Gọi $M$ là trung điểm của $BC$.
Vì $H$ đối xứng với $H'$ qua $I$ nên $M$ là trung điểm củ $HH'$
Xét tứ giác $HBH'C$ có hai đường chéo cắt nhau tại $M$ là trung điểm mỗi đường nên $HBH'C$ là hình bình hành
Do đó, \(BH'\parallel CH\), mà \(CH\perp AB\) (tính chất trực tâm)
\(\Rightarrow AB\perp BH'\Leftrightarrow \angle ABH'=90^0\), mà góc \(ABH'\) chắn cung $AH'$ nên $AH'$ chính là đường kính của đường tròn ngoại tiếp tam giác $ABC$
\(\Rightarrow A,H'\) đối xứng nhau qua $I$ ( $I$ chính là tâm đường tròn ngoại tiếp)
Akai Haruma qua trag của mình giải dùm mình 5 bài mới đăng đi. thanks
hãy tìm những chữ cái in hoa có tâm đối xứng. Và vẽ tâm dối xứng của các chữ cái in hoa đó
help meeeeeeeeeeeeeeeee
Các chữ in hoa có tâm đối xứng là H,N,O,I
