3 bạn A,B,C mỗi bạn viết ngẫu nhiên lên bảng 1 số tự nhiên thuộc đoạn [1;16]. Xác suất để 3 số được viết ra có tổng chia hết cho 3 bằng?
Cho em hỏi cách làm dạng này với ạ :<
Bài 6: Ôn tập chương Tổ hợp - Xác suất
Mỗi bạn có 16 cách viết nên số phần tử không gian mẫu là 16^3.
Gọi A là biến cố '3 số được viết ra có tổng chia hết cho 3'
Các số tự nhiên từ 1 đến 16 chia thành 3 nhóm:
Nhóm I gồm các số tự nhiên chia hết cho 3 gồm 5 số.
Nhóm II gồm các số tự nhiên cho 3 dư 1 gồm 6 số.
Nhóm III gồm các số tự nhiên cho 3 dư 2 gồm 5 số.
Để ba số có tổng chia hết cho 3 thì xảy ra các trường hơp sau:
Cả ba bạn viết được số thuộc nhóm I có 5^3 cách.
Cả ba bạn viết được số thuộc nhóm II có 6^3 cách.
Cả ba bạn viết được số thuộc nhóm III có 5^3 cách.
Mỗi bạn viết được một số thuộc một nhóm có 3!×(5×6×5)
=> n(A) = 5^3 + 6^3 + 5^3 + 3!×(5×6×5) = 1366
Vậy P(A) = 1366/16^3
Đúng 1
Bình luận (0)
Giúp em câu trả lời trắc nghiệm với ạ.
\(sinx-\sqrt{3}cosx=2\left(\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx\right)=2sin\left(x-\dfrac{\pi}{3}\right)=2sint\)
\(y=\sqrt{4sin^2t-4sint-m+3}\)
Hàm xác định trên R khi và chỉ khi:
\(4sin^2t-4sint-m+3\ge0\) ;\(\forall m\)
\(\Leftrightarrow m\le\min\limits_R\left(4sin^2t-4sint+3\right)\)
Ta có: \(4sin^2t-4sint+3=\left(2sint-1\right)^2+2\ge2\)
\(\Rightarrow m\le2\Rightarrow\) có 2 giá trị nguyên dương của m thỏa mãn
20.
Ngôn ngữ đề bài không rõ ràng, có "2 chữ cái giống nhau" ở đây nghĩa là "ít nhất 2 chữ cái giống nhau" hay "cả 2 cặp chữ cái giống nhau" đều đứng cạnh nhau
Không gian mẫu: \(\dfrac{6!}{2!.2!}=180\)
- Theo cách hiểu thứ 2:
Xếp 2 cặp chữ cái: 1 cách
Hoán vị 2 cặp này và 2 chữ còn lại: \(4!=24\) cách
Xác suất: \(P=\dfrac{24}{180}=\dfrac{2}{15}\)
- Theo cách hiểu thứ nhất:
Xếp 2 chữ cái cạnh nhau: 2 cách
Hoán vị 5 chữ cái: \(\dfrac{5!}{2!}=60\) cách
Số cách thỏa mãn: \(2.60-4!=96\)
Xác suất: \(P=\dfrac{96}{180}=\dfrac{8}{15}\)
Đúng 0
Bình luận (0)
Từ 12 học sinh gồm 5 học sinh giỏi, 4 học sinh khá, 3 học sinh trung bình. Giáo viên muốn thành lập 4 nhóm để làm 4 bài tập lớn, mỗi nhóm 3 học sinh. Tính xác xuất để nhóm nào cũng có học sinh giỏi và học sinh khá
Xem chi tiết
sorry,I am not T-T
28 tháng 12 2020 lúc 21:56
Có 3 loại kẹo gồm 10 kẹo dâu, 12 kẹo cam, 14 kẹo me, các kẹo cùng loại giống hệt nhau. Cô giáo muốn chia cho 18 học sinh, mỗi em gồm 2 cái khác loại. Hỏi cô giáo có bao nhiêu cách chia
Một hộp có chứa 6 cầu trắng và 4 cầu đen cùng kích thước. Lấy ngẫu nhiên cùng lúc 3 cầu. Tìm xác suất để trong 3 cầu lấy được:
a) Có 2 cầu đen;
b) Có ít nhất 2 cầu đen;
c) Toàn cầu trắng .
Không gian mẫu: \(C_{10}^3\)
a. Xác suất: \(\dfrac{C_4^2.C_6^1}{C_{10}^3}=...\)
b. \(P=\dfrac{C_4^2C_6^1+C_4^3}{C_{10}^3}=...\)
c. \(P=\dfrac{C_6^3}{C_{10}^3}=...\)
Đúng 0
Bình luận (0)
Câu 1. Cho tập , gọi là tập các số tự nhiên khác nhau có chữ số khác nhau được lập từ các số của tập . Chọn ngẫu nhiên một số trong tập , tính xác suất để chọn được số chia hết cho .
Đọc tiếp
Câu 1. Cho tập 
, gọi 
là tập các số tự nhiên khác nhau có 
chữ số khác nhau được lập từ các số của tập 
. Chọn ngẫu nhiên một số trong tập , tính xác suất để chọn được số chia hết cho .
Có mấy cách phân phối 15 phần thưởng cho 3 học sinh, sao cho học sinh thứ nhất có 2 phần thưởng, học sinh thứ hai có 3 phần thưởng và học sinh thứ ba có 10 phần thưởng. Các bạn giúp m với ạ
số cách phân phối phần thưởng là :
\(C_{15}^2\cdot C_{13}^3\cdot C_{10}^{10}\)
Đúng 1
Bình luận (0)
có hai lô hàng, mỗi lô có 10 sản phẩm. Lô I có 3 sản phẩm loại A. Lô II có 6 sản phẩm loại A.
1/ Nếu từ mỗi lô lấy ra 1 sản phẩm. Tính xác suất để hai sản phẩm lấy ra từ 2 lô:
a/ có đúng 1 sản phẩm loại A
b/ cùng loại
2/ Từ lô I lấy 3 sản phẩm bỏ sang lô II, rối từ lô II lấy ra 1 sản phẩm. Tính xác suất để sản phẩm lấy ra từ lô II là loại A
1/
a/ TH1: Lấy 1 sp loại A từ lô I có: \(C^1_3\) (cách)
Lấy 1 sp từ 4 sp còn lại từ lô II có: \(C^1_4\) (cách)
\(\Rightarrow C^1_3.C^1_4\) (cách)
TH2: Lấy 1 sp loại A từ lô II có: \(C^1_6\) (cách)
Lấy 1 sp từ 7 sp còn lại từ lô I có: \(C^1_7\) (cách)
\(\Rightarrow C^1_6.C^1_7\) (cách)
Không gian mẫu: \(n\left(\Omega\right)=C^1_{10}.C^1_{10}\)
\(\Rightarrow p\left(M\right)=\dfrac{C^1_6.C^1_7+C^1_3.C^1_4}{C_{10}^1.C^1_{10}}=0,54\)
b/ TH1: Lấy 1 sp loại A từ lô I: \(C^1_3\) (cách)
Lấy 1 sp loại A từ lô II: \(C^1_6\) (cách)
\(\Rightarrow C^1_3.C^1_6\) (cách)
TH2: Lấy 1 sp từ 7 sp còn lại trong lô I: \(C^1_7\) (cách)
Lấy 1 sp từ 4 sp còn lại trong lô II: \(C^1_4\) (cách)
\(\Rightarrow C^1_7.C^1_4\) (cách)
\(\Rightarrow p\left(O\right)=\dfrac{C_3^1.C_6^1+C^1_7.C^1_4}{C^1_{10}.C^1_{10}}=...\)
Bài 2 mình ko chắc nên ko làm nhé :(
Đúng 1
Bình luận (1)
hộp 1 có 10 sản phẩm tốt và 2 sản phẩm hỏng hộp 2 có 20 sản phẩm tốt và 4 sản phẩm hỏng. Từ hộp 1 lấy ra 1 sản phẩm bỏ qua hộp 2, sau đó từ hộp 2 lấy ra 1 sản phẩm .
a) Tính xác xuất sản phẩm từ hộp 2 là hỏng.
b) Nếu sản phẩm từ hộp 2 là hỏng, tính xác suất sản phẩm từ hộp 1 là tốt.
Giải giúp mình với ạ
Hoàn toàn không dịch được các kí hiệu mà bạn ghi
Để ghi kí hiệu tổ hợp bạn sử dụng công cụ soạn thảo này:
Sau đó gõ chữ hoa cần ghi (ví dụ C nếu muốn tổ hợp, A nếu muốn chỉnh hợp) rồi chọn tiếp chỗ này:
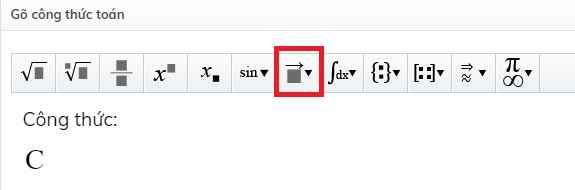
Sau đó chọn:
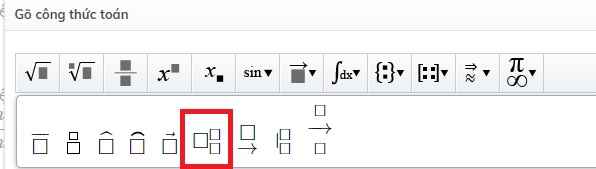
Rồi ghi giá trị k, n vào 2 ô nhỏ trên dưới là được
Đúng 0
Bình luận (1)