Cho tam giác MNP trung tuyến ME. Các đường phân giác của góc MEN và góc PEM lần lượt cắt các cạnh MN, MP tại C và D a) cmr: CD // NP b) gọi O là giao điểm của ME và CD. Cmr OC= OD
Bài 3: Tính chất đường phân giác của tam giác
a: Xét ΔMEN có EC là phân giác
nên MC/CN=ME/NE=ME/EP
Xét ΔMEP có ED là phân giác
nên MD/DP=ME/EP
=>MC/CN=MD/DP
=>CD//NP
b: Xét ΔMNE có OC//NE
nên OC/NE=MO/ME
Xét ΔMEP có OD//EP
nên OD/EP=MO/ME
=>OD/EP=OC/NE
mà EP=NE
nên OD=OC
Đúng 0
Bình luận (0)
Cho ▲ ABC cân tại A có BC =10cm,AC=40cm,đường phân giác BD
a) Tính độ dài AD,DC
b) Tính độ dài BD
Giups em vs ạ em cần đang cần câu trả lời gấp![]() em c.ơntrước ạ
em c.ơntrước ạ
a: Xét ΔBAC có BD là phân giác
nên AD/AB=DC/BC
=>AD/4=DC/1=(AD+DC)/(4+1)=40/5=8
=>AD=32cm; DC=8cm
b: Kẻ đường cao AH
=>H là trung điểm của BC
=>HB=HC=5cm
Xét ΔAHC vuông tại H có sin C=AH/AC=5/40=1/8
nên góc C=7 độ
\(BD=\dfrac{2\cdot40\cdot10}{40+10}\cdot\dfrac{cos\widehat{B}}{2}\simeq15,97\left(cm\right)\)
Đúng 0
Bình luận (1)
Cho ▲ ABC cân tại A có BC =10cm,AC=40cm,đường phân giác BD
a) Tính độ dài AD,DC
b) Tính độ dài BD
Giups em vs ạ em cần đang cần câu trả lời gấp![]() em c.ơntrước ạ
em c.ơntrước ạ
a: Xét ΔBAC có BD là phân giác
nên AD/AB=DC/BC
=>AD/4=DC/1=(AD+DC)/(4+1)=40/5=8
=>AD=32cm; DC=8cm
b: Kẻ đường cao AH
=>H là trung điểm của BC
=>HB=HC=5cm
Xét ΔAHC vuông tại H có sin C=AH/AC=5/40=1/8
nên góc C=7 độ
\(BD=\dfrac{2\cdot40\cdot10}{40+10}\cdot\dfrac{cos\widehat{B}}{2}\simeq15,97\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho ▲ ABC cân tại A có BC 10cm,AC40cm,đường phân giác BD a) Tính độ dài AD,DCb) Tính độ dài BDGiups em vs ạ em cần đang cần câu trả lời gấp em c.ơntrước ạ(em chx học cos nên ah/cj có thể đừng tl cos đc ko ạ)
Đọc tiếp
Cho ▲ ABC cân tại A có BC =10cm,AC=40cm,đường phân giác BD
a) Tính độ dài AD,DC
b) Tính độ dài BD
Giups em vs ạ em cần đang cần câu trả lời gấp![]() em c.ơntrước ạ(em chx học cos nên ah/cj có thể đừng tl cos đc ko ạ)
em c.ơntrước ạ(em chx học cos nên ah/cj có thể đừng tl cos đc ko ạ)
a: Xét ΔBAC có BD là phân giác
nên AD/AB=DC/BC
=>AD/4=DC/1=(AD+DC)/(4+1)=40/5=8
=>AD=32cm; DC=8cm
b: Kẻ đường cao AH
=>H là trung điểm của BC
=>HB=HC=5cm
Xét ΔAHC vuông tại H có sin C=AH/AC=5/40=1/8
nên góc C=7 độ
\(BD=\dfrac{2\cdot40\cdot10}{40+10}\cdot\dfrac{cos\widehat{B}}{2}\simeq15,97\left(cm\right)\)
Đúng 1
Bình luận (2)
Cho △ABC, các đường pgiac AD, BE, CF. Biết BC = 36cm, CA = 30cm, AB = 18cm. Tính độ dài các đoạn BD, DC, EA, EC, FA, FB.
Xét ΔABC co AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/5=(BD+DC)/(3+5)=36/8=4,5
=>BD=13,5cm; CD=22,5cm
Xét ΔBAC có BE là phân giác
nên EA/AB=EC/BC
=>EA/1=EC/2=(EA+EC)/(1+2)=30/3=10
=>EA=10cm; EC=20cm
Xét ΔABC có CF là phân giác
nên FA/AC=FB/BC
=>FA/30=FB/36
=>FA/5=FB/6=(FA+FB)/(5+6)=18/11
=>FA=90/11cm; FB=108/11cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường phân giác BD biết AD = 3 cm BC = 5 cm Tính độ dài AB,BC
Lời giải:
Áp dụng tính chất tia phân giác:
$\frac{AD}{DC}=\frac{AB}{BC}$
$\Leftrightarrow \frac{3}{DC}=\frac{AB}{5}$
$\Rightarrow 15=AB.DC=AB(AC-AD)=AB(AC-3)(1)$
Mà: $AB^2+AC^2=BC^2=25(2)$
Từ $(1); (2)\Rightarrow (\frac{15}{AC-3})^2=AB^2=25-AC^2$
$\Leftrightarrow AC^4-6AC^3-16AC^2+150AC=0$
$\Leftrightarrow AC^3-6AC^2-16AC+150=0$
PT giải ra số khá xấu. Bạn xem lại đề.
Đúng 0
Bình luận (0)
cho tam giác MNP có M=90 độ,MN=20cm,NP=29cm,phân giác NQ.Tính QM,QP
Xem chi tiết
\(MP=\sqrt{29^2-20^2}=21\left(cm\right)\)
Xét ΔNMP có NQ là phân giác
nên QM/MN=QP/NP
=>QM/20=QP/29=(QM+QP)/(20+29)=21/49=3/7
=>QM=60/7cm; QP=87/7(cm)
Đúng 0
Bình luận (0)
Cho ∆ABC. AD là đường phân giác (D thuộc BC). AB=4, AC=8. Tính DB, DC.
Không đủ dữ kiện để tính DB, DC. Bạn xem lại.
Đúng 0
Bình luận (0)
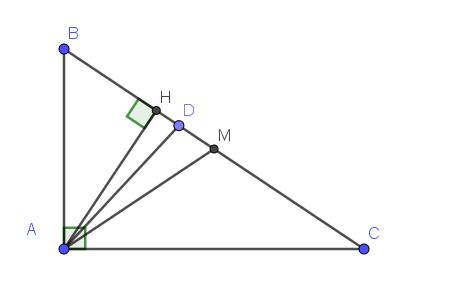
Cho tam giác ABC vuông tại A có AB=6, AC=8. Kẻ đường phân giác AD và trung tuyến AM. Tính diện tích tam giác ADM.
Lời giải:
Gọi chiều cao của tam giác là $AH$, $H\in BC$
Ta có:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (theo định lý Pitago)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8$
Vì $M$ là trung điểm của $BC$ nên $BM=CM=BC:2=10:2=5$
Áp dụng tính chất tia phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{6}{8}=\frac{3}{4}$
$\Rightarrow \frac{BD}{BC}=\frac{3}{7}$
$\Rightarrow BD=\frac{3}{7}.BC=\frac{30}{7}$
$MD=BM-BD=5-\frac{30}{7}=\frac{5}{7}$
$S_{ADM}=\frac{DM.AH}{2}=\frac{5.4,8}{7.2}=\frac{12}{7}$
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 3 AC = 4 AD là đường phân giác Tính a) Độ dài các đoạn thẳng BC,DB,DC
b) Khoảng cách từ điểm D đến đường thẳng AC
c) Độ dài đường phân giác AD help mik đang cần gấp mik cảm ơn
a: BC=5
Xet ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=5/7
=>DB=15/7; DC=20/7
c: \(AD=\dfrac{2\cdot3\cdot4}{3+4}\cdot cos45=\dfrac{12}{7}\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)