Question

Cho tam giác ABC vuông tại A có AB=6, AC=8. Kẻ đường phân giác AD và trung tuyến AM. Tính diện tích tam giác ADM.

Answer 1

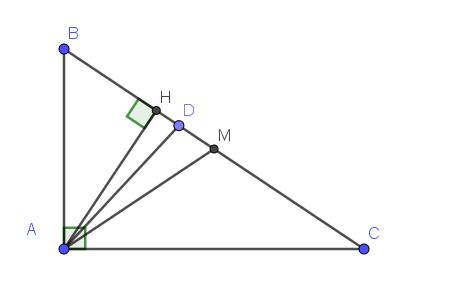
Lời giải:
Gọi chiều cao của tam giác là $AH$, $H\in BC$

Ta có:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (theo định lý Pitago)

$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8$ 

Vì $M$ là trung điểm của $BC$ nên $BM=CM=BC:2=10:2=5$ 

Áp dụng tính chất tia phân giác:

$\frac{BD}{DC}=\frac{AB}{AC}=\frac{6}{8}=\frac{3}{4}$

$\Rightarrow \frac{BD}{BC}=\frac{3}{7}$

$\Rightarrow BD=\frac{3}{7}.BC=\frac{30}{7}$

$MD=BM-BD=5-\frac{30}{7}=\frac{5}{7}$

$S_{ADM}=\frac{DM.AH}{2}=\frac{5.4,8}{7.2}=\frac{12}{7}$ 

Answer 2

Hình vẽ: