Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng

Ta có hình vẽ câu a , câu b:

chúc bạn học tốt

@Nguyễn Huy Tú

câu 3

A1=110^o(đối đỉnh)

A2+A4=180^o(kề bù)

 =>A2=70^o

A3=70^o

B3=55^o(đối đỉnh)

B3+B1=180^o(kề bù)

 B1=125^o

B4=125^o(đối đỉnh)

Bài 3: 

\(\widehat{A_2}=70^0;\widehat{A_3}=70^0;\widehat{A_1}=110^0\)

\(\widehat{B_4}=125^0;\widehat{B_1}=125^0;\widehat{B_3}=55^0\)

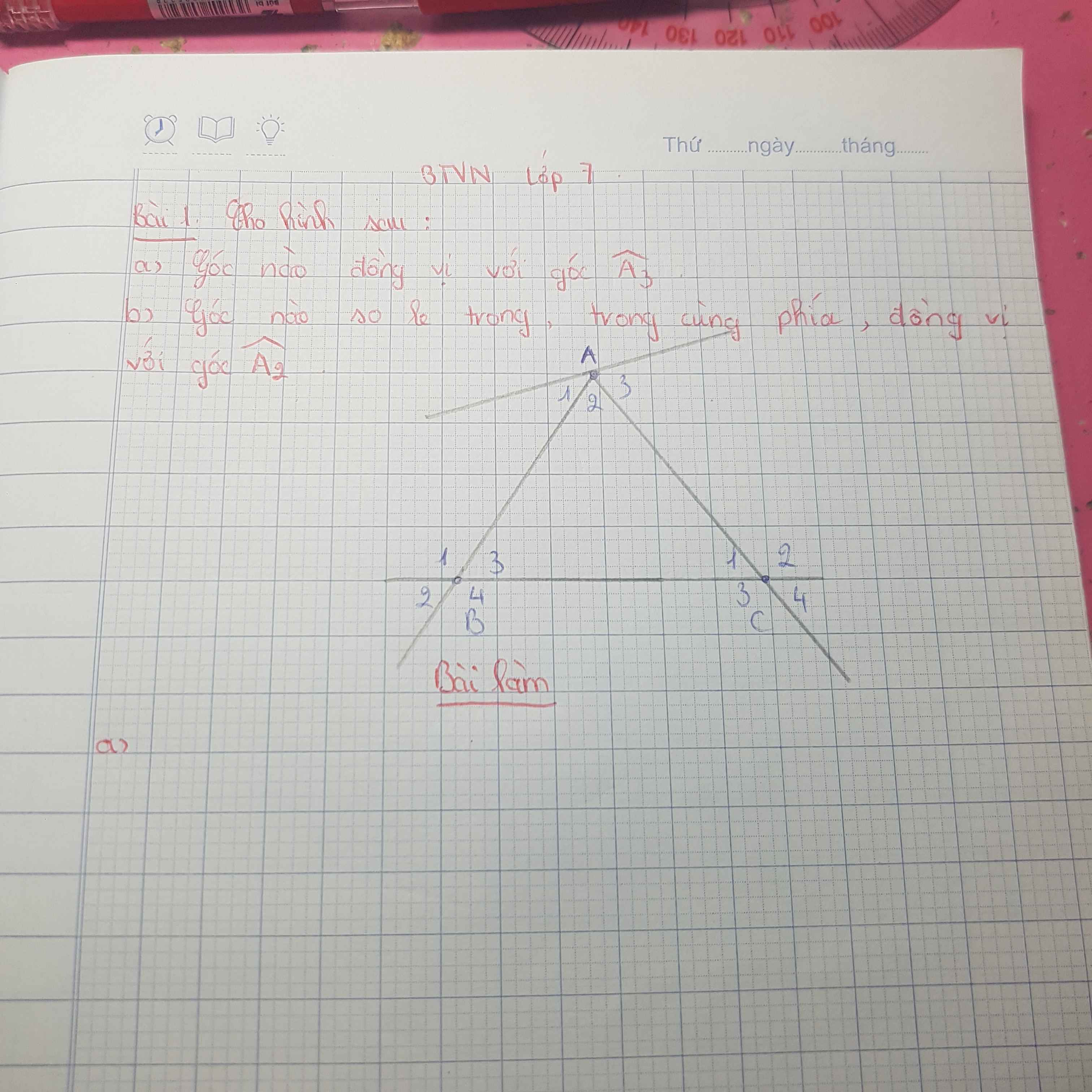
a) Góc đồng vị với góc A3 là góc C4

b) Góc so le trong với góc A2 là góc B1 và góc C2

Góc trong cùng phía với góc A2 là góc B3 và góc C1

Góc đồng vị với góc A2 là góc B4 và góc C3

Ta có: d' // d''

=> góc C₁ = góc E₁ = 60⁰ (slt)

Ta có: d' // d''

=> góc D₁ = góc G₂ = 110⁰ (đồng vị)

Ta có: góc G₂ + góc G₃ = 180⁰ (kề bù)

hay 110⁰ + góc G₃ = 180⁰

=> góc G₃ = 180⁰ - 110⁰ = 70⁰

Ta có: góc D₁ = góc D₄ = 110⁰ (đối đỉnh)

Ta có: d//d''

=> góc E₁ = góc A₅ = 60⁰ (đồng vị)

Ta có: d//d''

=> góc G₃ = góc B₆ = 70⁰ (đồng vị).

Vì d'//d'' => ^E₁=^C₁=60 độ (2 góc so le trong)

Vì d'//d'' => ^G₂=^D₁=110 độ (2 góc đồng vị)

Ta có: ^D₁=^D₄ =110 độ (đối đỉnh)

Mà d'//d'' => ^G₃=70 độ (^G₃ và ^D₄ là 2 góc trong cùng phía)

Vì d//d' => ^A₅=^C₁=60 độ (2 góc so le ngoài)

Vì d//d'' => ^B₆=^G₃=70 độ (2 góc đồng vị)

*Tính \(\widehat{E_1}\)

Ta có : d' // d"

Vì \(\widehat{E_1}\) và \(\widehat{C_1}\) là 2 góc so le trong .

\(\Rightarrow\widehat{E_1}=\widehat{C_1}=60^o\)

*Tính \(\widehat{G_2}\)

Ta có : d' // d"

Vì \(\widehat{D_1}\) và \(\widehat{G_2}\) là 2 đồng vị .

\(\Rightarrow\widehat{D_1}=\widehat{G_2}=110^o\)

*Tính \(\widehat{G_3}\)

Vì \(\widehat{G_3}\) và \(\widehat{G_2}\) là 2 góc kề bù.​​​

\(\Rightarrow\widehat{D_3}+\widehat{G_2}=180^o\)

\(\Rightarrow\widehat{G_3}+110^o=180^o\)

\(\Rightarrow\widehat{G_3}=180^o-110^o=70^o\)

*Tính \(\widehat{D_4}\)

Ta có : d' // d"

Vì \(\widehat{G_2}\) và \(\widehat{D_4}\) là 2 đồng vị .

\(\widehat{G_2}=\widehat{D_4}=110^o\)

*Tính \(\widehat{A_5}\)

Ta có : d' // d"

Vì \(\widehat{A_5}\) và \(\widehat{E_1}\) là 2 đồng vị .

\(\Rightarrow\widehat{A_5}=\widehat{E_1}=60^o\)

*Tính \(\widehat{B_6}\)

\(\Rightarrow\widehat{B_6}=\widehat{G_3}=70^o\)

Hình:

Giải:

+ Vì \(\widehat{AOC}< \widehat{AOB}\left(40^0< 180^0\right)\)

Nên OC là tia nằm giữa hai tia OA và OB

Ta có đẳng thức:

\(\widehat{AOC}+\widehat{BOC}=\widehat{AOB}\)

\(\Leftrightarrow40^0+\widehat{BOC}=180^0\)

\(\Leftrightarrow\widehat{BOC}=180^0-40^0=140^0\)

+ Vì \(\widehat{BOD}< \widehat{BOC}\left(50^0< 140^0\right)\)

Nên OD là tia nằm giữa hai tia OC và OB

Ta có đẳng thức:

Hình bị che mất rồi làm sao mà tìm được nên vẽ lại hình đi