Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng
Nội dung lý thuyết
1, Góc so le trong. Góc đồng vị.
Cho hình vẽ sau:

Trong hình vẽ trên, đường thẳng \(a\) căt hai đường thẳng \(b\), \(c\) lần lượt tại \(A\) và \(B\) tạo thành bốn góc đỉnh \(A\), bốn góc đỉnh \(B\) được kí hiệu lần lượt như trên. Ta có:
- Các cặp góc \(\widehat{A_3}\) và \(\widehat{B_1}\), \(\widehat{A_4}\) và \(\widehat{B_2}\) là các cặp góc so le trong.
- Các cặp góc \(\widehat{A_1}\) và \(\widehat{B_1}\), \(\widehat{A_2}\) và \(\widehat{B_2}\), \(\widehat{A_3}\) và \(\widehat{B_3}\), \(\widehat{A_4}\) và \(\widehat{B_4}\) là các cặp góc đồng vị.
@54404@@54406@
2. Tính chất.
Trong hình vẽ dưới đây, cho \(\widehat{A_4}=\widehat{B_1}=60^0\)
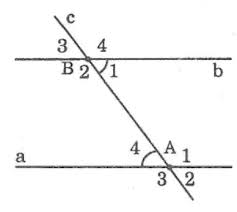
- Do \(\widehat{A_1}\) và \(\widehat{A_4}\) là hai góc kề bù nên \(\widehat{A_1}=180^0-\widehat{A_4}=180^0-60^0=120^0\)
Dó \(\widehat{B_1}\) và \(\widehat{B_2}\) là hai góc kề bù nên \(\widehat{B_2}=180^0-\widehat{B_1}=180^0-60^0=120^0\)
Ta biết rằng \(\widehat{A_1}\) và \(\widehat{B_2}\) cũng là một cặp góc so le trong và khi đó \(\widehat{A_1}=\widehat{B_2}=120^0\)
- Do \(\widehat{A_2}\) và \(\widehat{A_4}\) là hai góc đối đỉnh nên \(\widehat{A_2}=\widehat{A_4}=60^0\)
Do \(\widehat{B_1}\) và \(\widehat{B_3}\) là hai góc đối đỉnh nên \(\widehat{B_1}=\widehat{B_3}=60^0\).
Ta biết rằng \(\widehat{A_4}\) và \(\widehat{B_3}\) là hai góc đồng vị và khi đó \(\widehat{A_4}=\widehat{B_3}=60^0\).
Từ đó ta rút ra tính chất:
Nếu đường thẩng \(c\) cắt hai đường thẳng \(a\), \(b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
a) Hai góc so le trong còn lại bằng nhau;
b) Hai góc đồng vị bằng nhau.
@54409@
Ví dụ: Cho hình vẽ sau. BIết góc \(\widehat{H_3}=\widehat{K_1}=120^0\). Tính các góc còn lại đỉnh \(H\)?
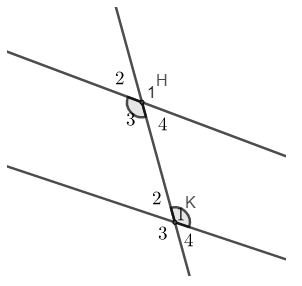
Ta có \(\widehat{K_1}\) và \(\widehat{K_2}\) là hai góc kề bù \(\Rightarrow\) \(\widehat{K_1}+\widehat{K_2}=180^0\Rightarrow\widehat{K_2}=180^0-\widehat{K_1}=180^0-120^0=60^0\)
Do \(\widehat{H_3}\) và \(\widehat{K_1}\) là hai góc so le trong mà \(\widehat{H_3}=\widehat{K_1}\). Áp dụng tính chất nêu trên ta có:
\(\widehat{H_4}=\widehat{K_2}=60^0\) (cặp góc so le trong còn lại bằng nhau)
\(\widehat{H_1}=\widehat{K_1}=120^0\) ; \(\widehat{H_2}=\widehat{K_2}=60^0\) (hai góc đồng vị bằng nhau)