Bài 1: Định lý Talet trong tam giác

Theo định lý Ta - let ta có:

   \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\) 

\(\Leftrightarrow\dfrac{4}{6}=\dfrac{3}{AC}\) 

\(\Rightarrow\dfrac{2}{3}=\dfrac{1}{AC}\) 

\(\Rightarrow2AC=3\) 

\(\Rightarrow AC=\dfrac{2}{3}\) 

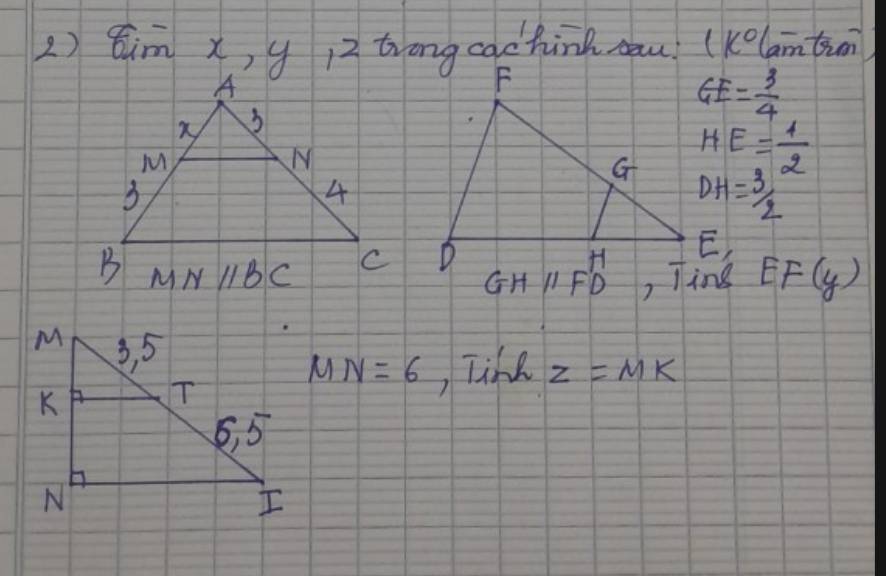
Hình 1:

Xét ΔABC có MN//BC

nên \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)

=>\(\dfrac{x}{3}=\dfrac{3}{4}\)

=>\(x=\dfrac{3}{4}\cdot3=2,25\)

Hình 2:

EH+HD=ED

=>ED=0,5+1,5=2

Xét ΔEFD có GH//FD

nên \(\dfrac{EG}{EF}=\dfrac{EH}{ED}\)

=>\(\dfrac{0.75}{EF}=\dfrac{0.5}{2}=\dfrac{1}{4}\)

=>EF=0,75*4=3

=>y=3

Hình 3:

Xét ΔMNI có KT//NI

nên \(\dfrac{MK}{MN}=\dfrac{MT}{MI}\)

=>\(\dfrac{6}{MN}=\dfrac{3.5}{10}\)

=>\(MN=6\cdot\dfrac{10}{3.5}=\dfrac{60}{3.5}=\dfrac{120}{7}\)

=>\(z=\dfrac{120}{7}\)

a: OM//CD

=>OM/CD=AO/AC=AM/AD

ON//DC

=>ON/CD=BO/BD=BN/BC

b: OM/CD=ON/CD(AM/AD=BN/BC)

=>OM=ON

c: 2/MN=1/AB+1/CD

=>2/MN=1/4+1/6=3/12+2/12=5/12

=>MN/2=12/5

=>MN=24/5=4,8cm

Xét ΔDAC có MI//AC
nên \(\dfrac{DI}{DC}=\dfrac{DM}{DA}\)

mà \(\dfrac{DM}{DA}=\dfrac{BN}{BC}\)

nên \(\dfrac{DI}{DC}=\dfrac{DM}{DA}=\dfrac{BN}{BC}\)

=>Các tỉ số bằng với tỉ số DI/DC là \(\dfrac{DM}{DA};\dfrac{BN}{BC}\)

a: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=6^2+8^2=100=10^2\)

=>BC=10(cm)

Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DB}{6}=\dfrac{DC}{8}\)

=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)

mà DB+DC=BC=10cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{10}{7}\)

=>\(DB=3\cdot\dfrac{10}{7}=\dfrac{30}{7}\left(cm\right);DC=4\cdot\dfrac{10}{7}=\dfrac{40}{7}\left(cm\right)\)

b: 

Kẻ DH\(\perp\)AC

=>DH là khoảng cách từ D đến AC

DH\(\perp\)AC

AB\(\perp\)AC

Do đó: DH//AB

Xét ΔCAB có DH//AB

nên \(\dfrac{DH}{AB}=\dfrac{CD}{CB}\)

=>\(\dfrac{DH}{6}=\dfrac{40}{7}:10=\dfrac{4}{7}\)

=>\(DH=\dfrac{24}{7}\)(cm)

c: Xét ΔABC có AD là phân giác

nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)\)

\(=\dfrac{2\cdot6\cdot8}{6+8}\cdot cos45\)

\(=\dfrac{24\sqrt{2}}{7}\left(cm\right)\)

Ta có:

\(\dfrac{AB}{AD}=\dfrac{6}{4}=\dfrac{3}{2}\)

\(\dfrac{AC}{AE}=\dfrac{9}{6}=\dfrac{3}{2}\)

\(\Rightarrow\dfrac{AB}{AD}=\dfrac{AC}{AE}=\dfrac{3}{2}\)

Xét 2 tam giác ABC và tam giác ADE ta có: 

\(\widehat{CAB}\) chung 

\(\dfrac{AB}{AD}=\dfrac{AC}{AE}\left(=\dfrac{3}{2}\right)\) 

\(\Rightarrow\Delta ABC\sim\Delta ADE\left(c.g.c\right)\)

\(\Rightarrow\dfrac{DE}{BC}=\dfrac{AB}{AD}=\dfrac{AC}{AE}=\dfrac{3}{2}\)

Vậy: ... 

Bài 8:

a: Xét ΔBAC có EF//BC

nên \(\dfrac{BE}{EA}=\dfrac{BF}{FC}\)

=>\(\dfrac{BF}{FC}=2\)

=>\(\dfrac{CF}{FB}=\dfrac{1}{2}\)

Xét ΔCDB có GF//BD

nên \(\dfrac{CF}{FB}=\dfrac{CG}{GD}\)

=>\(\dfrac{CG}{GD}=\dfrac{1}{2}\)

=>\(\dfrac{DG}{CG}=2\)

Xét ΔDAC có GH//AC

nên \(\dfrac{DH}{AH}=\dfrac{DG}{CG}=2\)

=>\(\dfrac{AH}{DH}=\dfrac{1}{2}\)

b: Xét ΔABD có \(\dfrac{AE}{EB}=\dfrac{AH}{HD}\)

nên EH//BD

c: Ta có: EH//BD

GF//BD

Do đó: EH//GF

Ta có: EF//AC

GH//AC

Do đó: EF//GH

Xét tứ giác EFGH có

EF//GH

EH//GF

Do đó: EFGH là hình bình hành

AQ:CQ=5:8

=>\(\dfrac{AQ}{5}=\dfrac{CQ}{8}\)

mà CQ-AQ=9

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AQ}{5}=\dfrac{CQ}{8}=\dfrac{CQ-AQ}{8-5}=\dfrac{9}{3}=3\)

=>\(AQ=5\cdot3=15cm;CQ=8\cdot3=24cm\)