cho a,b,c>0 thỏa mãn a+b+c=3.
CMR:(ab)5 +(bc)5+(ca)5>=\(\sqrt{\left(abc\right)^3}\).(ab+bc+ca)
Kính nhờ mọi người hỗ trợ em ạ
cho a,b,c>0 thỏa mãn a+b+c=3.
CMR:(ab)5 +(bc)5+(ca)5>=\(\sqrt{\left(abc\right)^3}\).(ab+bc+ca)
Kính nhờ mọi người hỗ trợ em ạ
Cho a, b, c > 0 và abc = 1. Chứng minh rằng \(\dfrac{1}{a^2.\left(b+c\right)}+\dfrac{1}{b^2.\left(c+a\right)}+\dfrac{1}{c^2.\left(a+b\right)}\ge\dfrac{3}{2}\)
Đặt \(x=\dfrac{1}{a},y=\dfrac{1}{b},z=\dfrac{1}{c}\) khi đó thu được \(xyz=1\)
Ta có:
\(\dfrac{1}{a^2\left(b+c\right)}=\dfrac{x^2}{\dfrac{1}{y}+\dfrac{1}{z}}=\dfrac{x^2yz}{y+z}=\dfrac{x}{y+z}\)
BĐT cần chứng minh được viết lại thành:\(\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}\ge\dfrac{3}{2}\)
\(\Leftrightarrow\left(\dfrac{x}{y+z}+1\right)+\left(\dfrac{y}{z+x}+1\right)+\left(\dfrac{z}{x+y}+1\right)\ge\dfrac{9}{2}\)
\(\Leftrightarrow\left(x+y+z\right)\left(\dfrac{1}{y+z}+\dfrac{1}{z+x}+\dfrac{1}{x+y}\right)\ge\dfrac{9}{2}\)
Đánh giá cuối cùng đúng theo BĐT Cauchy
Vậy BĐT được chứng minh. Đẳng thức xảy ra khi và chỉ khi a = b = c = 1.
Cho a,b,c dương tm \(a+b\le c\). Tìm GTNN của \(P=\left(a^4+b^4+c^4\right)\left(\dfrac{1}{4a^4}+\dfrac{1}{4b^4}+\dfrac{1}{c^4}\right)\)
\(P=\dfrac{x\left(4x^2+3\right)+y\left(4y^2+3\right)}{x+y+4xy}\)
Với \(0\le a;bc\le1\), chứng minh rằng \(\dfrac{a}{1+b.c}+\dfrac{b}{1+c.a}+\dfrac{c}{1+a.b}+\dfrac{abc}{2}\le2\)
P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán gợi ý và giúp đỡ em với ạ!
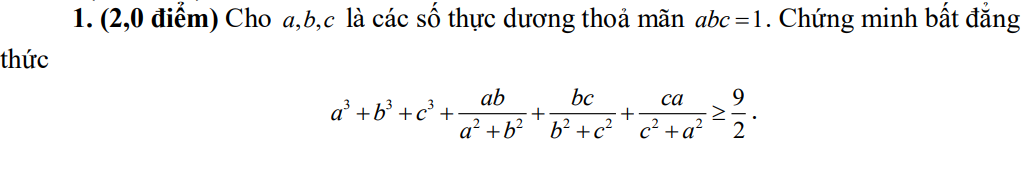 Help me!!! Cần gấp ạ. Cảm ơn trc nha!!!
Help me!!! Cần gấp ạ. Cảm ơn trc nha!!!
Giải cho e Câu 1: tự luận với
\(A=cos10^o.cos50^o.cos70^o=\dfrac{cos10^o}{2}\left[cos120^o+cos20^o\right]=\dfrac{cos10^o}{2}\left[cos20^o-\dfrac{1}{2}\right]\)
\(=\dfrac{1}{2}\left[cos10^o.cos20^o-\dfrac{1}{2}cos10^o\right]\)
\(=\dfrac{1}{2}\left[\dfrac{1}{2}\left(cos30^o+cos10^o\right)-\dfrac{1}{2}cos10^o\right]=\dfrac{1}{4}.\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{8}\)
\(B=\left(cos\dfrac{\pi}{5}+cos\dfrac{4\pi}{5}\right)+\left(cos\dfrac{2\pi}{5}+cos\dfrac{3\pi}{5}\right)\)
\(=2cos\dfrac{\pi}{2}.cos\dfrac{3\pi}{10}+2cos\dfrac{\pi}{2}.cos\dfrac{\pi}{10}=0\)
\(C=cos\dfrac{2\pi}{7}+cos\dfrac{4\pi}{7}+cos\dfrac{6\pi}{7}\)
\(\Rightarrow C.sin\dfrac{\pi}{7}=sin\dfrac{\pi}{7}.cos\dfrac{2\pi}{7}+sin\dfrac{\pi}{7}.cos\dfrac{4\pi}{7}+sin\dfrac{\pi}{7}.cos\dfrac{6\pi}{7}\)
\(=\dfrac{1}{2}\left[sin\dfrac{3\pi}{7}+sin\dfrac{-\pi}{7}+sin\dfrac{5\pi}{7}+sin\dfrac{-3\pi}{7}+sin\pi+sin\dfrac{-5\pi}{7}\right]\)
\(=\dfrac{1}{2}\left(sin\pi-sin\dfrac{\pi}{7}\right)=-\dfrac{1}{2}sin\dfrac{\pi}{7}\) \(\Rightarrow C=-\dfrac{1}{2}\)