§5. Dấu của tam thức bậc hai
Nội dung lý thuyết
I. ĐỊNH LÍ VỀ DẤU CỦA TAM THỨC BẬC HAI
1. Tam thức bậc hai
Tam thức bậc hai đối với \(x\) là biểu thức có dạng \(f\left(x\right)=ax^2+bx+c\), trong đó \(a,b,c\) là các hệ số, \(a\ne0\).
Ví dụ: +) \(f_1\left(x\right)=2x^2-3x+5\) ;
+) \(f_2\left(x\right)=\dfrac{1}{2}x^2-2x+\dfrac{3}{4}\) ;
+) \(f_3\left(x\right)=-x^2-\dfrac{x}{3}+\dfrac{5}{3}\) ; ...
2. Dấu của tam thức bậc hai
Ví dụ: Xét Parabol \(y=f\left(x\right)=x^2-5x+4\):
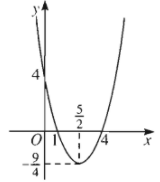
Nhận xét: \(\Delta=b^2-4ac=\left(-5\right)^2-4.1.4=9>0\)
Parabol có đỉnh \(I\left(\dfrac{5}{2};-\dfrac{9}{4}\right)\), nghịch biến trên khoảng \(\left(-\infty;\dfrac{5}{2}\right)\), đồng biến trên khoảng \(\left(\dfrac{5}{2};+\infty\right)\);
Với \(x=1\) hoặc \(x=4\) thì \(f\left(x\right)=0\) ;
Với \(1< x< 4\) thì \(f\left(x\right)< 0\), đồ thị hàm số nằm phía dưới trục hoành ;
Với \(x< 1\) hoặc \(x>4\) thì \(f\left(x\right)>0\), đồ thị hàm số nằm phía trên trục hoành.
Người ta đã chứng minh được định lí về dấu của tam thức bậc hai như sau:
Cho \(f\left(x\right)=ax^2+bx+c\) (\(a\ne0\)), \(\Delta=b^2-4ac\).
Nếu \(\Delta< 0\) thì \(f\left(x\right)\) luôn cùng dấu với hệ số \(a\), với mọi \(x\in R\).
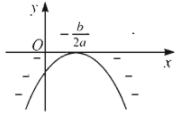
Nếu \(\Delta=0\) thì \(f\left(x\right)\) luôn cùng dấu với hệ số \(a\), trừ khi \(x=-\dfrac{b}{2a}\).
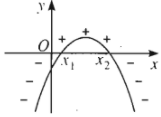
Nếu \(\Delta>0\) thì \(f\left(x\right)\) cùng dấu với hệ số \(a\) khi \(x< x_1\) hoặc \(x>x_2\), trái dấu với hệ số \(a\) khi \(x_1< x< x_2\) trong đó \(x_1,x_2\left(x_1< x_2\right)\) là hai nghiệm của \(f\left(x\right)\).
Chú ý: Trong định lí trên ta có thể thay biệt thức \(\Delta=b^2-4ac\) bằng biệt thức thu gọn \(\Delta'=\left(b'\right)^2-ac\).
Minh hoạ bằng hình học:
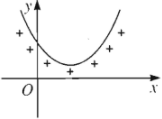
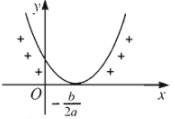
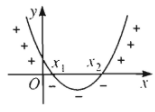
Với \(a>0\):
| \(\Delta< 0\) | \(\Delta=0\) | \(\Delta>0\) |
|
|
|
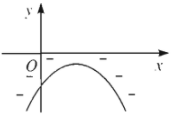
Với \(a< 0\):
| \(\Delta< 0\) | \(\Delta=0\) | \(\Delta>0\) |
|
|
|
3. Áp dụng
Ví dụ 1: Xét dấu của tam thức \(f\left(x\right)=-x^2+3x-5\).
Giải:
Ta có: \(\Delta=3^2-4.\left(-1\right).\left(-5\right)=-11< 0\), hệ số \(a=-1< 0\)
Do đó \(f\left(x\right)< 0\) với mọi \(x\).
Ví dụ 2: Lập bảng xét dấu của tam thức \(f\left(x\right)=2x^2-5x+2\).
Giải:
Ta có: \(\Delta=\left(-5\right)^2-4.2.2=9>0\), hệ số \(a=2>0\)
\(f\left(x\right)\) có hai nghiệm phân biệt \(x_1=\dfrac{1}{2}\), \(x_2=2\).
Theo định lí về dấu của tam thức bậc hai ta có bảng xét dấu:
| \(x\) | \(-\infty\) \(\dfrac{1}{2}\) \(2\) \(+\infty\) |
| \(f\left(x\right)\) | + \(0\) - \(0\) + |
@1892944@
Tương tự như tích, thương của nhị thức bậc nhất, ta cũng có thể xét dấu tích, thương của các tam thức bậc hai.
Ví dụ 3: Xét dấu biểu thức \(f\left(x\right)=\dfrac{2x^2-x-1}{x^2-4}\).
Giải:
Ta lần lượt xét dấu của tam thức \(g\left(x\right)=2x^2-x-1\) và \(h\left(x\right)=x^2-4\) sau đó lập bảng xét dấu.
Xét \(g\left(x\right)=2x^2-x-1\):
Ta có: \(\Delta=\left(-1\right)^2-4.2.\left(-1\right)=9>0\), hệ số \(a=2>0\), \(g\left(x\right)\) có 2 nghiệm phân biệt là \(x_1=-\dfrac{1}{2}\) và \(x_2=1\).
Do đó: Với \(x< -\dfrac{1}{2}\) hoặc \(x>1\) thì \(g\left(x\right)>0\), với \(-\dfrac{1}{2}< x< 1\) thì \(g\left(x\right)< 0\).
Xét \(h\left(x\right)=x^2-4\):
Ta có: \(\Delta=0^2-4.1.\left(-4\right)=16>0\), hệ số \(a=1>0\), \(h\left(x\right)\) có 2 nghiệm phân biệt là \(x_1=-2\) và \(x_2=2\).
Do đó: Với \(x< -2\) hoặc \(x>2\) thì \(h\left(x\right)>0\), với \(-2< x< 2\) thì \(h\left(x\right)< 0\).
Từ đó ta có bảng xét dấu:
| \(x\) | \(-\infty\) \(-2\) \(-\dfrac{1}{2}\) \(1\) \(2\) \(+\infty\) |
| \(g\left(x\right)=2x^2-x-1\) | + \(|\) + \(0\) - \(0\) + \(|\) + |
| \(h\left(x\right)=x^2-4\) | + \(0\) - \(|\) - \(|\) - \(0\) + |
| \(f\left(x\right)\) | + \(|\)\(|\) - \(0\) + \(0\) - \(|\)\(|\) + |
Kết luận: \(f\left(x\right)>0\) khi \(x< -2\) hoặc \(-\dfrac{1}{2}< x< 1\) hoặc \(x>2\) ;
\(f\left(x\right)< 0\) khi \(-2< x< -\dfrac{1}{2}\) hoặc \(1< x< 2\) ;
\(f\left(x\right)=0\) khi \(x=-\dfrac{1}{2}\) hoặc \(x=1\) ;
\(f\left(x\right)\) không xác định khi \(x=-2\) hoặc \(x=2\).
II. BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
1. Bất phương trình bậc hai
Bất phương trình bậc hai ẩn \(x\) là bất phương trình dạng \(ax^2+bx+c< 0\) (hoặc \(ax^2+bx+c\le0\), \(ax^2+bx+c>0\), \(ax^2+bx+c\ge0\)), trong đó \(a,b,c\) là các số thực đã cho, \(a\ne0\).
Ví dụ: +) \(2x^2+x-3< 0\) ;
+) \(\dfrac{1}{3}x^2-2x+\dfrac{2}{5}\ge0\) ;
+) \(x^2-25\le0\) ; ...
2. Giải bất phương trình bậc hai
Giải bất phương trình bậc hai \(ax^2+bx+c< 0\) thực chất là tìm các khoảng mà trong đó \(f\left(x\right)=ax^2+bx+c\) cùng dấu với hệ số \(a\) (trường hợp \(a< 0\)) hoặc trái dấu với hệ số \(a\) (trường hợp \(a>0\)).
Ví dụ 4: Giải các bất phương trình:
a) \(-2x^2+3x+5>0\) ;
b) \(-3x^2+7x-4< 0\) ;
c) \(9x^2-24x+16\ge0\).
Giải:
a) Xét tam thức \(f\left(x\right)=-2x^2+3x+5\) có:
\(\Delta=3^2-4.\left(-2\right).5=49>0\) , hệ số \(a=-2< 0\)
Tam thức có 2 nghiệm là \(x_1=-1\), \(x_2=\dfrac{5}{2}\)
Do vậy tam thức luôn dương với mọi \(x\in\left(-1;\dfrac{5}{2}\right)\),
Vậy bất phương trình \(-2x^2+3x+5>0\) có tập nghiệm là \(\left(-1;\dfrac{5}{2}\right)\).
b) Xét tam thức \(f\left(x\right)=-3x^2+7x-4\) có:
\(\Delta=7^2-4.\left(-3\right).\left(-4\right)=1>0\) , hệ số \(a=-3< 0\)
Tam thức có 2 nghiệm phân biệt là \(x_1=1\), \(x_2=\dfrac{4}{3}\)
Do vậy tam thức luôn âm với mọi \(x\) thuộc khoảng \(\left(-\infty;1\right)\) hoặc \(\left(\dfrac{4}{3};+\infty\right)\)
Vậy bất phương trình \(-3x^2+7x-4< 0\) có tập nghiệm là \(\left(-\infty;1\right)\cup\left(\dfrac{4}{3};+\infty\right)\).
c) Xét tam thức \(f\left(x\right)=9x^2-24x+16\) có:
\(\Delta'=\left(-12\right)^2-9.16=0\) , hệ số \(a=9>0\)
Tam thức có nghiệm kép \(x_1=x_2=\dfrac{4}{3}\)
Do đó \(f\left(x\right)>0\) với mọi \(x\ne\dfrac{4}{3}\) ; \(f\left(x\right)=0\) với \(x=\dfrac{4}{3}\)
Như vậy bất phương trình \(9x^2-24x+16\ge0\) nghiệm đúng với mọi \(x\).
@1893082@
Ví dụ 5: Tìm các giá trị của tham số \(m\) để phương trình sau có 2 nghiệm trái dấu:
\(2x^2-\left(m^2-m+1\right)x+2m^2-3m-5=0\) (*)
Giải:
Gọi \(x_1,x_2\) là 2 nghiệm của phương trình (*)
Theo hệ thức Vi-ét ta có: \(x_1.x_2=\dfrac{c}{a}\)
Để \(x_1,x_2\) trái dấu nhau khi và chỉ khi \(a\) và \(c\) trái dấu, tức là \(m\) phải thoả mãn điều kiện \(2\left(2m^2-3m-5\right)< 0\)
\(\Leftrightarrow2m^2-3m-5< 0\)
Xét tam thức \(f\left(m\right)=2m^2-3m-5\) ta có:
\(\Delta=\left(-3\right)^2-4.2.\left(-5\right)=49>0\), tam thức có 2 nghiệm phân biệt là \(m_1=-1\) và \(m_2=\dfrac{5}{2}\), hệ số \(a=2>0\)
Do đó \(f\left(m\right)< 0\Leftrightarrow-1< m< \dfrac{5}{2}\)
Kết luận: Vậy phương trình đã cho có 2 nghiệm trái dấu khi và chỉ khi \(-1< m< \dfrac{5}{2}\).
@1893221@