Các câu hỏi tương tự
câu 1 trong các phương trình sau, phương trình nào là phương trình chính tắc của elip(vì sao)
a) x 2 9 + y 2 6 =1 b) x 2 25 + y 2 16 = 1
c) x 2 4 + y 2 9 =1 c) X 2 8 + y 2 2 =1
1)Xét sự biến thiêna)yx2019+1 trên (âm vô cùng, dương vô cùng)b)yfrac{1}{x-2} trên (âm vô cùng, 2) ; (2, dương vô cùng)2)Tìm tính chất đặc trưng:A{frac{3}{4} , frac{8}{9} , frac{15}{16} , frac{24}{25} , frac{35}{36} }B{frac{4}{5},frac{9}{10},frac{16}{17},frac{25}{26},frac{37}{36} }
Đọc tiếp
1)Xét sự biến thiên
a)y=x2019+1 trên (âm vô cùng, dương vô cùng)
b)y=\(\frac{1}{x-2}\) trên (âm vô cùng, 2) ; (2, dương vô cùng)
2)Tìm tính chất đặc trưng:
A={\(\frac{3}{4}\) , \(\frac{8}{9}\) , \(\frac{15}{16}\) , \(\frac{24}{25}\) , \(\frac{35}{36}\) }
B={\(\frac{4}{5},\frac{9}{10},\frac{16}{17},\frac{25}{26},\frac{37}{36}\) }
Cho đường tròn (C) (x-1)2 + (y-1)2 = 25
(Cm) (x-2)2 + (y-m)2 = 16
Gọi m1, m2 là các giá trị thỏa mãn khoảng cách giữa hai giao điểm của C và Cm là lớn nhất Khẳng định nào sau đấy đúng
A. 1« m1 + m2 < 4
B. -1 « m1 + m2 <1
C. m1 + m2 » 4
D. m1 + m2 <-1
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip (E) có phương trình chính tắc \(\dfrac{x^2}{25}+\dfrac{y^2}{9}=1\). Độ dài trục lớn của elip (E) là:
A. 10 B. 25 C. 9 D. 6
Viết phương trình tiếp tuyến chung của hai đường tròn: (C1) : (x -5) 2+ (y+12) 2 225 và (C2) : (x-1)2+ (y-2)2 25.
Đọc tiếp
Viết phương trình tiếp tuyến chung của hai đường tròn: (C1) : (x -5) 2+ (y+12) 2= 225 và (C2) : (x-1)2+ (y-2)2= 25.
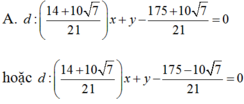
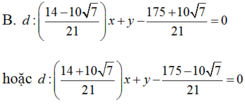
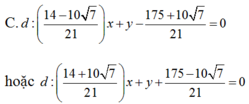
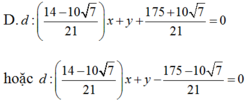
tìm điều kiện bài toán:
a) \(y=\dfrac{1}{x}-\dfrac{\sqrt{2x-1}}{x^2-3x+2}\)
b) \(y=\dfrac{1}{x^2-1}-\sqrt{7-2x}\)
c) \(y=\dfrac{2}{x}+\dfrac{3}{4-2x+x^2}\)
d) \(y=\sqrt{25-x^2}-2\sqrt{x}+3\)
PHẦN TỰ LUẬN: Bài 1: Cho A={ x€R| (x^4 -16)(x² -1)=0} và B={x€N| 2x-9≤0}. Tìm tập hợp X sao cho: X⊂B\A Bài 2: Cho tập hợp A={-1;1;5;8}, B="gồm các ước số nguyên dương của 16"
Chứng minh rằng
\(\frac{\sqrt[2016]{9}+\sqrt[2016]{16}+\sqrt[2016]{25}}{\sqrt[2016]{12}+\sqrt[2016]{15}+\sqrt[2016]{20}}>\frac{\sqrt[2017]{12}+\sqrt[2017]{15}+\sqrt[2017]{20}}{\sqrt[2017]{9}+\sqrt[2017]{16}+\sqrt[2017]{25}}\)
đường tròn (C) có đường kính AB với A(6;-3), B(1;2) có phương trình là:A. (x-dfrac{7}{2})^2+(y+dfrac{1}{2})^2dfrac{50}{4} B.(x-7)^2+(y+1)^250C. (x-dfrac{7}{2})^2+(y+dfrac{1}{2})^225 D. (x-7)^2+(y+1)^225
Đọc tiếp
đường tròn (C) có đường kính AB với A(6;-3), B(1;2) có phương trình là:
A. \((x-\dfrac{7}{2})^2\)+\((y+\dfrac{1}{2})^2\)=\(\dfrac{50}{4}\) B.\((x-7)^2\)+\((y+1)^2\)=50
C. \((x-\dfrac{7}{2})^2\)+\((y+\dfrac{1}{2})^2\)=25 D. \((x-7)^2\)+\((y+1)^2=25\)










