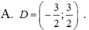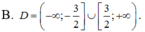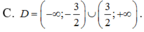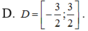Với điều kiện x >0, ta có: log( x log 9 ) = log( 9 logx )
log( x log 9 ) = log9.logx và log( 9 logx ) = logx.log9
Nên log( x log 9 ) = log 9 logx )
Suy ra: x log 9 = 9 logx
Đặt t = x log 9 , ta được phương trình 2t = 6 ⇔ t = 3 ⇔ x log 9 = 3
⇔ log( x log 9 ) = log3
⇔log9.logx = log3
⇔logx = log3/log9 ⇔ logx = 1/2
⇔ x = 10 (thỏa mãn điều kiện x > 0)