Chọn B.
Ta có: Δ = (m - 2 ) 2 - (m - 1)(m - 3) = ( m 2 - 4m + 4 ) - ( m 2 - 4m + 3) = 1 > 0
Phương trình có hai nghiệm phân biệt x1, x2.
Áp dụng hệ thức Vi-ét ta có:
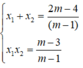
Ta có:
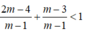
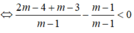
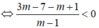
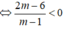
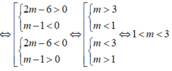
Chọn B.
Ta có: Δ = (m - 2 ) 2 - (m - 1)(m - 3) = ( m 2 - 4m + 4 ) - ( m 2 - 4m + 3) = 1 > 0
Phương trình có hai nghiệm phân biệt x1, x2.
Áp dụng hệ thức Vi-ét ta có:
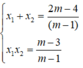
Ta có:
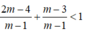
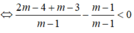
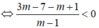
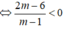
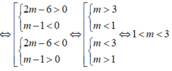
Cho phương trình: x 2 - 2(m - 3)x + 5 - m = 0
a) Giải phương trình khi m = 1.
b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn x1 < x2 < 1.
Cho phương trình \(x^2-2\left(m+1\right)x+m^2+2m=0\) (với m là tham số). Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1,x2(x1<x2)
thoa man: \(\left|x1\right|=3\left|x2\right|\)
Tìm m để phương trình x 2 + 2 ( m + 1 ) x + 2 ( m + 6 ) = 0 có hai nghiệm x 1 , x 2 mà x 1 + x 2 = 4
A. m = 1
B. m = -3
C. m = -2
D. Không tồn tại m
Cho phương trình x 2 - 2 m + 1 x + m 2 + 2 = 0 với m là tham số. Tìm m để phương trình có hai nghiệm x 1 ; x 2 sao cho A = x 1 x 2 − 2 ( x 1 + x 2 ) − 6 đạt giá trị nhỏ nhất
A. m =2
B. m = 1 2
C. m=1
D. m = 4 ± 10
Cho phương trình \(x^2-2\left(m-1\right)x+m^2-3=0\) với m là tham số. Tìm m để phương trình có hai nghiệm \(x_1\)\(x_2\) sao cho \(A=2\left(x1^2+x2^2\right)-x1.x2\) đạt giá trị lớn nhất
\(B=\frac{x1.x2}{x1^2+x2^2-x1.x2}\) đạt giá trị nhỏ nhất
Cho phương trình : x2 - 4mx +9(m-1)2 = 0
a. Xem xét với các giá trị nào của m thì phương trình trên có nghiệm ?
b. Giả sử x1, x2 là nghiệm của phương trình đã cho, hãy tính tổng và tích của chúng. Tìm một hệ thức giữa x1 và x2 không phụ thuộc vào m.
c. Xác định giá trị của m để hiệu các nghiệm của phương trình bằng 4.
Cho phương trình: mx ^2 - 2(m-1)x + 3(m-2) = 0.Tìm giá trị của tham số m để 2 nghiệm x1; x2 thỏa mãn: x1+2x2=1
Cho phương trình x2+ 2( m+ 3) x+ m2-3=0, m là tham số.
Tìm m để phương trình có hai nghiệm x1; x2 và P = 5( x1+ x2) – 2x1.x2 giá trị lớn nhất.
A. m= -1
B. m= -2
C. m=0
D. m=1
Cho phương trình x 2 - 2 ( m + 1 ) x + m 2 + 2 = 0 với m là tham số. Tìm m để phương trình có hai nghiệm x 1 ; x 2 sao cho B = 2 ( x 1 2 + x 2 2 ) + 16 − 3 x 1 x 2 đạt giá trị lớn nhất
A. m =2
B. m = 1 2
C. m=1
D. m = 4 ± 10