Các câu hỏi tương tự
Với a và b là hai số thực dương tùy ý, log (ab2) bằng
![]()
![]()
![]()
![]()
Với a là số thực dương tùy ý khác 1, giá trị của
log
a
3
a
bằng: A. 3 B. C. D. –3
Đọc tiếp
Với a là số thực dương tùy ý khác 1, giá trị của log a 3 a bằng:
A. 3
B. ![]()
C. ![]()
D. –3
Cho hàm số
f
(
x
)
l
n
(
e
x
+
m
)
. Có bao nhiêu số thực dương m để
f
a
+
f
b
1
với mọi số thực a,b thỏa mãn a+b1 A. 1 B. 2 C. Vô số D. 0
Đọc tiếp
Cho hàm số f ( x ) = l n ( e x + m ) . Có bao nhiêu số thực dương m để f ' a + f ' b = 1 với mọi số thực a,b thỏa mãn a+b=1
A. 1
B. 2
C. Vô số
D. 0
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi tùy ý sao cho
a
2
+
b
2
+
c
2
3
. Khoảng cách từ O đến mặt phẳng (ABC) lớn nhất bằng A.
1
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi tùy ý sao cho a 2 + b 2 + c 2 = 3 . Khoảng cách từ O đến mặt phẳng (ABC) lớn nhất bằng
A. 1 3
B. 3
C. 1 3
D. 1
Biết
∫
1
3
2
+
ln
(
x
+
3
)
(
x
+
1
)
2
d
x
a
ln
2
+
b
ln...
Đọc tiếp
Biết ∫ 1 3 2 + ln ( x + 3 ) ( x + 1 ) 2 d x = a ln 2 + b ln 3 + c ( a , b , c ∈ ℚ ) . Giá trị 3a-b+2c bằng
A. 7
B. 0
C. -2
D. - 11 2
Biết
∫
0
1
2
x
2
+
3
x
+
3
x
2
+
2
x
+
1
d
x
a
-
ln
b
với a, b là các số nguyên dương. Tính
P...
Đọc tiếp
Biết ∫ 0 1 2 x 2 + 3 x + 3 x 2 + 2 x + 1 d x = a - ln b với a, b là các số nguyên dương. Tính P = a 2 + b 2 .
A. 13.
B. 5.
C. 4.
D. 10.
Cho x, y là các số thực dương thỏa mãn
ln
x
+
ln
y
≥
ln
x
2
+
y
. Tính giá trị nhỏ nhất của P x + y.
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn ln x + ln y ≥ ln x 2 + y . Tính giá trị nhỏ nhất của P = x + y.
![]()
![]()
![]()
![]()
Với các số thực dương x,y tùy ý , đặt
log
3
x
a
,
log
3
y
b
. Mệnh đề nào dưới đây là đúng ?
Đọc tiếp
Với các số thực dương x,y tùy ý , đặt log 3 x = a , log 3 y = b . Mệnh đề nào dưới đây là đúng ?
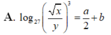
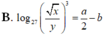
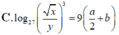
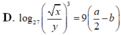
Với a, b là các số thực dương tùy ý và a khác 1, đặt
P
log
a
b
3
+
log
a
2
b
6
Mệnh đề nào dưới đây đúng ? A.
P
9
log
a
b
B. P 27...
Đọc tiếp
Với a, b là các số thực dương tùy ý và a khác 1, đặt P = log a b 3 + log a 2 b 6 Mệnh đề nào dưới đây đúng ?
A. P = 9 log a b
B. P = 27 log a b 15
C. P = 15 log a b
D. P = 6 log a b



