Các câu hỏi tương tự
Cho lục giác lồi A_1A_2A_3A_4A_5A_6 có diện tích bằng 1 và có các cặp cạnh đối song song, hai đường thẳng A_6A_1; A_2A_3 cắt nhau tại điểm B_1, hai đường thẳng A_1A_2;A_3A_4 cắt nhau tại điểm B_2.;...; tương tự, A_{i-1}A_i;A_{i+1}A_{i+2} cắt nhau tại điểm B_i (xem A_7 là A_1 và A_8 là A_2). Chứng minh rằng tổng diện tích của sáu tam giác A_iB_iA_{i+1}, i1,...,6 không bé hơn 1.
Đọc tiếp
Cho lục giác lồi \(A_1A_2A_3A_4A_5A_6\) có diện tích bằng 1 và có các cặp cạnh đối song song, hai đường thẳng \(A_6A_1\); \(A_2A_3\) cắt nhau tại điểm \(B_1\), hai đường thẳng \(A_1A_2;A_3A_4\) cắt nhau tại điểm \(B_2\).;...; tương tự, \(A_{i-1}A_i;A_{i+1}A_{i+2}\) cắt nhau tại điểm \(B_i\) (xem \(A_7\) là \(A_1\) và \(A_8\) là \(A_2\)). Chứng minh rằng tổng diện tích của sáu tam giác \(A_iB_iA_{i+1}\), \(i=1,...,6\) không bé hơn 1.
Cho đường thẳng \(d:2mx+\left(m-1\right)y-2=0\) và \(d':\left(m+2\right)x+\left(2m+1\right)y-\left(m+2\right)=0\)Tìm m để:
a, 2 đường thẳng cắt nhau
b, 2 đường thẳng song song
c, 2 đường thẳng trùng nhau
Cho hình thang ABCD, hai đường chéo AC và BD cắt nhau tại O. Qua O kẻ MN song song với AB (AB là đáy của hình thang, M∈AD ,N∈BC). Đặt
A
B
→
a
;
D
C
→
b
. Khi đó khẳng định nào sau đây là đúng? A.
M
N
→...
Đọc tiếp
Cho hình thang ABCD, hai đường chéo AC và BD cắt nhau tại O. Qua O kẻ MN song song với AB (AB là đáy của hình thang, M∈AD ,N∈BC). Đặt A B → = a ; D C → = b . Khi đó khẳng định nào sau đây là đúng?
A. M N → = a A B → + b D C → a + b
B. M N → = b A B → + a D C → a + b
C. M N → = a A B → - b D C → a + b
D. M N → = b A B → - a D C → a + b
Bài 4 : ( 3,5 điểm) Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O; R) (với AB AC). BE và CF là 2 đường cao của tam giác cắt nhau tại Ha) Chứng minh tứ giác BEFC và AEHF là tứ giác nội tiếpb) Đường thẳng EF cắt đường thẳng BC tại S và EF cắt đường tròn (O) tại M và N (M nằm giữa S và E). Chứng minh SM. SN SE. SFc) Tia CE cắt đường tròn (O) tại K, vẽ dây KI song song với EF.Chứng minh H, K đối xứng nhau qua ABd) Chứng minh 3 điểm H, F, I thẳng hàng.
Đọc tiếp
Bài 4 : ( 3,5 điểm) Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O; R) (với AB < AC). BE và CF là 2 đường cao của tam giác cắt nhau tại H
a) Chứng minh tứ giác BEFC và AEHF là tứ giác nội tiếp
b) Đường thẳng EF cắt đường thẳng BC tại S và EF cắt đường tròn (O) tại M và N (M nằm giữa S và E). Chứng minh SM. SN = SE. SF
c) Tia CE cắt đường tròn (O) tại K, vẽ dây KI song song với EF.
Chứng minh H, K đối xứng nhau qua AB
d) Chứng minh 3 điểm H, F, I thẳng hàng.
Cho đường thẳng d: y= (m-1) x+m và d’: y= (m2-1) x+ 6 . Có bao nhiêu giá trị của m để hai đường thẳng d; d’ song song với nhau.
A. 0
B. 1
C. 2
D. 3
Cho đường thẳng d: y = (m − 1)x + mvà d′: y = ( m 2 − 1)x + 6. Tìm m để hai đường thẳng d, d′ song song với nhau
A. m = 0 và m = 3
B. m = 0 và m = 2
C. m = 0 và m = 1
D. m = 0 và m = 4
Trong các phát biểu sau a. Trực tâm là giao điểm của ba đường phân giác. b. Hình bình hành có hai đường chéo bằng nhau. c. Hình thoi có hai đường chéo vuông góc. d. Trọng tâm là giao điểm của ba đường trung tuyến. e. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường. Các phát biểu đúng là: A. b, c, d B. c, d, e C. a, c, d, e D. c, d
Đọc tiếp
Trong các phát biểu sau
a. Trực tâm là giao điểm của ba đường phân giác.
b. Hình bình hành có hai đường chéo bằng nhau.
c. Hình thoi có hai đường chéo vuông góc.
d. Trọng tâm là giao điểm của ba đường trung tuyến.
e. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Các phát biểu đúng là:
A. b, c, d
B. c, d, e
C. a, c, d, e
D. c, d
Tìm tham số m để hai đường thẳng d: m 2 x - 2y + 4 + m = 0 và Δ: 2x - y + 3 = 0 song song với nhau.
A. m = 4
B. m = 2
C. m = -2
D. m = 2 va m = -2
Vị trí tương đối của hai đường thẳng 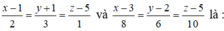
A. Cắt nhau
B. song song
C. chéo nhau
D. trùng nhau