A E B ^ có đỉnh E nằm bên ngoài đường tròn
⇒ A E B ^ = 1 2 . s đ A B ⏜ - s đ P Q ⏜ < 1 2 . s đ A B ⏜ = A C B ^

A E B ^ có đỉnh E nằm bên ngoài đường tròn
⇒ A E B ^ = 1 2 . s đ A B ⏜ - s đ P Q ⏜ < 1 2 . s đ A B ⏜ = A C B ^
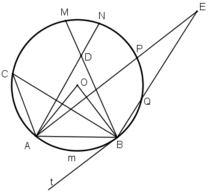
Trong hình 67, cung AmB có số đo là 60 ° . Hãy:
a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.
b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.
c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.
d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh ADB và ACB
e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh cung AEB với cung ACB
Câu 3(3đ) Cho nửa đường tròn tâm O,đường kính AB. Vẽ các tiếp tuyến Ax , By cùng phía với nửa đường tròn đối với AB. Qua điểm E thuộc nửa đường tròn (E khác A và B) kẽ tiếp tuyến với nửa đường tròn, nó cắt Ax , By theo thứ tự ở C và D
a)Chứng minh rằng : CD = AC + BD b)Tính số đo góc ? c)Tính : AC.BD ( Biết OA = 6cm)
Cho đường tròn (O;R) . Qua điểm A bên ngoài đường tròn ta vẽ các tiếp tuyến AB và AC với vòng tròn ( B và C là các tiếp điểm ) .Vẽ cát tuyến AEF ( E và B cùng thuộc một nữa mặt phẳng bờ OA , E nằm giữa A và F ) .Gọi D là trung điểm của E F . Gọi H là giao điểm của OA và BC .
1/. Chứng minh tứ giác ODBC nội tiếp.
2/. Vẽ đường kính BK của (O) . Gọi M là hình chiếu của C lên BK . AK cắt CM tại I. Chứng minh I là trung điểm của CM.
3/. Tia CM cắt (O) tại điểm thứ hai là N ,AN cắt (O) tại điểm thứ hai là J .CJ cắt AB tại Z .Chứng minh ZH vuông góc với OC .
Từ điểm A ở bên ngoài đường tròn (O), kẻ 2 tiếp tuyến AB, AC đến đường tròn (O) (B, C là 2 tiếp điểm). Kẻ cát tuyến ADE với đường tròn (O) (D nằm giữa A và E).
b) Chứng minh OA vuông góc với BC tại H và OD^2 = OH.OA. Từ đó suy ra tam giác OHD đồng dạng với tam giác ODA
c) C/m tam giác ABD đồng dạng với tam giác AEB
Cho nửa đường tròn có đường kính AB=2R. Vẽ các tiếp tuyến Ax, By với nửa đường tròn và tia Oz vuông góc với AB. ( các tia Ax, By, Oz cùng phía với nửa đường tròn đối với AB). Gọi E là điểm bất kì của nửa đường tròn. Qua E vẽ tiếp tuyến với nửa đường tròn , cắt Ax, By, Oz theo thứ tự ở C,D,M. Chứng minh rằng khi điểm E thay đổi vị trí trên đường tròn thì điểm M chạy trên một tia.
Cho (O). Từ một điểm I nằm ngoài (O), vẽ hai tia Ix,Iy không qua O; cắt đường tròn (O) theo thứ tự ở A, B, và C D sao cho góc OIx <góc OIy
a) so sánh AB và CD
b)vẽ đường tròn tâm O, bán kính OI cắt Ix, Iy lần lượt tại E,F. So sánh IA và BE, cung nhỏ IE và cung nhỏ IF.
Toán 9 nhé
BÀI 1 Cho đường tròn ( O) đường kính AB , vẽ bán kính OC vuông góc với AB. Từ B vẽ tiếp tuyến Bx. Gọi M là trung điểm OC , AM kéo dài cắt đường tròn tại E và Bx tại I .Tiếp tuyến từ E cắt Bx tại D. Chứng minh tứ giác MODE nội tiếp
BÀI 2: Cho đường tròn (O) đường kính AB, từ A và B vẽ Ax vuông góc với AB và By vuông góc BA ( Ax và By cùng phía so với bờ AB) .Vẽ tiếp tuyến x'My' ( tiếp điểm M ) cắt Ax tại C và By tại D; OC cắt AM tại I và OD cắt BM tại K .Chứng minh tứ giác CIKD nội tiếp
Từ điểm A ở bên ngoài đường tròn (O), kẻ 2 tiếp tuyến AB, AC đến đường tròn (O) (B, C là 2 tiếp điểm). Kẻ cát tuyến ADE với đường tròn (O) (D nằm giữa A và E).
b) Chứng minh OA vuông góc với BC tại H và OD^2 = OH.OA. Từ đó suy ra tam giác OHD đồng dạng với tam giác ODA
c) C/m tam giác ABD đồng dạng với tam giác AEB
từ một điểm M nằm ngoài đường tròn tâm O , vẽ 2 tiếp tuyến MA , MB với đường tròn (A,B là 2 tiếp điểm ).Trên dây AB lấy điểm H (H khác A và B).Qua H vẽ đường thẳng vuông góc với OH cắt đường thẳng MA ở E, cắt đoạn thẳng MB tại F
1. chứng minh tứ giác có 4 đỉnh O,H,A,E là tứ giác nội tiếp.
2.chứng minh tam giác OEF cân.
3.kẻ OI vuông góc với AB ( I THUỘC AB).chứng minh OI.OF=OB.OH