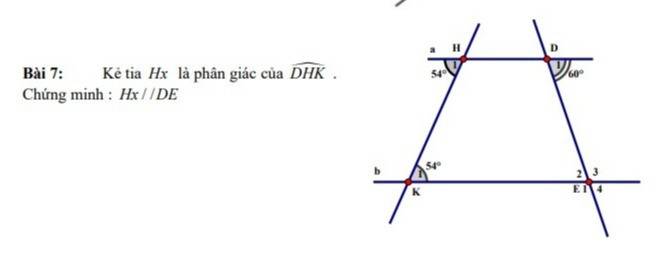
vẽ + giải
vẽ + giải
Bài 4. Cho tam giác \( ABC \) có ba góc nhọn, \( AB < AC \). Qua trung điểm \( D \) của cạnh \( BC \) kẻ đường thẳng vuông góc với tia phân giác của góc \( BAC \) cắt các đường thẳng \( AB \) và \( AC \) lần lượt tại \( H \) và \( K \).
a) Chứng minh tam giác \( AHK \) cân.
b) Qua \( B \) kẻ đường thẳng song song với \( AC \) cắt \( HK \) tại \( I \). Chứng minh rằng tam giác \( BHI \) cân.
c) Chứng minh \( BH = CK \).
Bài 5. Cho tam giác \( ABC \) cân tại \( A \), góc \( A \) tù. Trên tia đối của \( AB \) và \( AC \) lần lượt lấy \( M, N \) sao cho \( AM = AN < AB \). Gọi \( O \) là giao điểm của hai đường thẳng \( BN \) và \( CM \). Chứng minh rằng:
a) Tam giác \( OBC \) cân
b) \( \overline{ONC} = \overline{OMB} \).
c) \( OM = ON \).
d) Tia \( OA \) là phân giác của \( \angle BOC \).