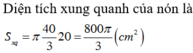Các câu hỏi tương tự
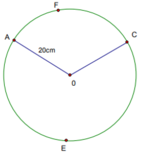
Tính thể tích V của khối nón có đáy là hình tròn bán kính 2, diện tích xung quanh của nón là 12
π
.
Đọc tiếp
Tính thể tích V của khối nón có đáy là hình tròn bán kính 2, diện tích xung quanh của nón là 12 π .
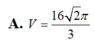
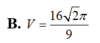
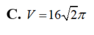
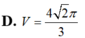
Một hình nón có đường kính đáy là 2a
π
3, góc ở đỉnh 120
°
. Thể tích của khối nón đó theo a là:A. 2
3
π
a
3
B. 3
π
a
3
C.
π
a
3
D.
π...
Đọc tiếp
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Một tấm bìa hình tròn có bán kính bằng 5 được cắt thành hai hình quạt, sau đó quấn hai hình quạt đó thành hai hình nón (không có đáy). Biết một trong hai hình nón này có diện tích xung quanh là
15
π
. Tính thể tích hình nón còn lại. Giả sử chiều rộng các mép dán không đáng kể.
Đọc tiếp
Một tấm bìa hình tròn có bán kính bằng 5 được cắt thành hai hình quạt, sau đó quấn hai hình quạt đó thành hai hình nón (không có đáy). Biết một trong hai hình nón này có diện tích xung quanh là 15 π . Tính thể tích hình nón còn lại. Giả sử chiều rộng các mép dán không đáng kể.
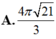
![]()
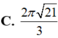
![]()
Diện tích xung quanh của hình trụ có bán kính đáy a và đường cao a
3
là:A. 2
π
a
2
3
B. 2
π
a
2
C.
π
a
2
D.
π
a...
Đọc tiếp
Diện tích xung quanh của hình trụ có bán kính đáy a và đường cao a 3 là:
A. 2 π a 2 3 B. 2 π a 2
C. π a 2 D. π a 2 3
Chia tấm bìa hình tròn bán kính R30 cm thành 3 phần (như hình vẽ). lấy một phần và uốn thành một hình nón có đường sinh là bán kính của hình tròn trên. Khi đó thể tích của khối nón tạo thành là A.
2
π
R
3
2
81
B.
π
R
3
27
C...
Đọc tiếp
Chia tấm bìa hình tròn bán kính R=30 cm thành 3 phần (như hình vẽ). lấy một phần và uốn thành một hình nón có đường sinh là bán kính của hình tròn trên. Khi đó thể tích của khối nón tạo thành là
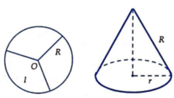
A. 2 π R 3 2 81
B. π R 3 27
C. 2 π R 3 2 27
D. π R 3 81
Hình nón có góc ở đỉnh là 9
0
o
và có diện tích xung quanh là π
2
. Độ dài đường cao của hình nón là: A. 1 B.
2
C. 1/
2
D. 2
Đọc tiếp
Hình nón có góc ở đỉnh là 9 0 o và có diện tích xung quanh là π 2 . Độ dài đường cao của hình nón là:
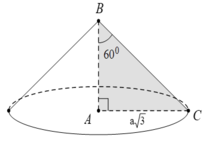
A. 1
B. 2
C. 1/ 2
D. 2
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi
S
1
là diện tích 6 mặt của hình lập phương,
S
2
là diện tích xung quanh của hình trụ. Tỉ số
S
2
/
S
1
bằng:A.
π...
Đọc tiếp
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
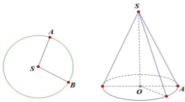
Cho hình tròn tâm S, bán kính R 2 . Cắt đi
1
4
hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón như hình vẽ. Tính diện tích toàn phần của hình nón đó.
Đọc tiếp
Cho hình tròn tâm S, bán kính R = 2 . Cắt đi 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón như hình vẽ. Tính diện tích toàn phần của hình nón đó.
![]()
![]()
![]()
![]()
Cho hình tròn tâm S, bán kính R 2. Cắt bỏ
1
4
hình tròn rồi dán lại để tạo ra mặt xung quanh của một hình nón N. Tính diện tích toàn phần
S
t
p
của hình nón N.
Đọc tiếp
Cho hình tròn tâm S, bán kính R = 2. Cắt bỏ 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của một hình nón N. Tính diện tích toàn phần S t p của hình nón N.
![]()
![]()
![]()