(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC) (2)
(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung CB) (5)
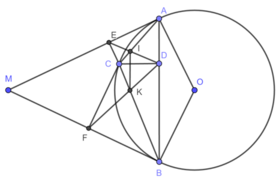
Từ một điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD, CE, CF lần lượt vuông góc với AB, MA, MB. Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh rằng: IK ⊥ CD
Từ một điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD, CE, CF lần lượt vuông góc với AB, MA, MB. Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh rằng: Tứ giác ICKD nội tiếp được
Từ một điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD, CE, CF lần lượt vuông góc với AB, MA, MB. Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh rằng: Các tứ giác AECD, BFCD nội tiếp được
Bài 4: Từ một điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy điểm C. Vẽ CD, CE, CF lần lượt vuông góc với AB, MA, MB. Gọi I là giao điểm AC và DE, K là giao điểm của BC và DF.
Chứng minh rằng :
a) Các tứ giác AECD, BFCD nội tiếp.
b) CD^2 =CE.CF.
c) Tứ giác ICKD nội tiếp được đường tròn.
d) IK _|_ CD
Từ một điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD, CE, CF lần lượt vuông góc với AB, MA, MB. Gọi I la giao điễm của AC và DE, K là giao điểm của BC và DF.
a. vẽ hình
b. 1) Chứng minh các tứ giác AECD, BFCD nội tiếp được.
2) CD2= CE.CF
3) Tứ giác ICKD nội tiếp được
4) IK vuông góc với CD
Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB với đường tròn (A, B là hai tiếp điểm). Lấy điểm C trên cung nhỏ AB (C không trùng với A và B). Từ điểm C kẻ CD vuông góc với AB, CE vuông góc với MA, CF vuông góc với MB( D ∈ A B , E ∈ M A , F ∈ M B ) . Gọi I là giao điểm của AC và DE K là giao điểm của BC và DF. Chứng minh rằng
1) Tứ giácABCE nội tiếp một đường tròn.
2) Hai tam giác CDE & CFD đồng dạng.
3) Tia đối của tia CD là tia phân giác góc E C F ⏞
4) Đường thẳng IK song song với đường thẳng AB
cho đường tròn (o) . Từ điểm M ở bên ngoài (O)vẽ hai tiếp tuyến MA, MB vs (O) (A,B là hai tiếp điểm). Trên cung nhỏ AB lấy một điểm C, gọi D,E,F lần lượt là hình chiếu vuông góc của điểm C lên các đoạn thẳng AB,MA,MB.
A)cm các tứ giác AECD, BFCD là tứ giác nội tiếp. Xác định tâm và bán kính của các đường tròn ngoại tiếp hai tứ giác đó
b) cm CD2= CE.CF
C) Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. CM 4 điểm I,C,K,D cùng thuộc một đường tròn
d) CM IK cuông góc vs CD
Từ điểm M nằm bên ngoài đường tròn (o), ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy điểm C. Vẽ CD, CE, CF lần lượt vuông góc với AB,MA,MB.
a, CM: AECD,BFCD nội tiếp
b, CD2=CE.CF
Từ điểm M nằm ngoài đường tròn tâm O, kẻ 2 tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB, lấy điểm C kẻ CD vuông góc với AB, CE vuông góc với AM, CF vuông góc với BM. Gọi I, K lần lượt là giao điểm của AC với DE, của BC với DF. Chứng minh:
a) AECD nội tiếp (ko cần)
b) CD^2=CE.CF (ko cần)
c) Tia đối của CD là tia phân giác của góc FCE
d) IK // AB
