Các câu hỏi tương tự
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và OAa, OB b, OC c. Tính thể tích khối tứ diện OABC A. abc B.
a
b
c
3
C.
a
b
c
6
D.
a
b
c
2
Đọc tiếp
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và OA=a, OB = b, OC =c. Tính thể tích khối tứ diện OABC
A. abc
B. a b c 3
C. a b c 6
D. a b c 2
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và OA OB a, OC2a. Thể tích khối cầu ngoại tiếp tứ diện OABC bằng A.
8
π
a
3
9
B.
2
π
a
3
C.
8...
Đọc tiếp
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và OA =OB =a, OC=2a. Thể tích khối cầu ngoại tiếp tứ diện OABC bằng
A. 8 π a 3 9
B. 2 π a 3
C. 8 π a 3 3
D. 6 π a 3
Thể tích của khối tứ diện OABC có OAOB OC a và OA,OB,OC đôi một tạo với nhau một góc
60
o
bằng A.
a
3
6
B.
a
3
3
C....
Đọc tiếp
Thể tích của khối tứ diện OABC có OA=OB= OC =a và OA,OB,OC đôi một tạo với nhau một góc 60 o bằng
A. a 3 6
B. a 3 3
C. 2 a 3 12
D. 2 a 3 4
Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc với nhau, biết OA3, OB4 và thể tích khối tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC) bằng: A. 3
Đọc tiếp
Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc với nhau, biết OA=3, OB=4 và thể tích khối tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC) bằng:
A. 3
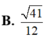
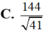
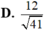
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA
a
2
2
, OB OC a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC) Tính thể tích khối tứ diện OABH A.
a
3
2
6
B.
a...
Đọc tiếp
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA = a 2 2 , OB= OC =a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC) Tính thể tích khối tứ diện OABH
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Cho khối tứ diện OABC với OA, OB, OC từng đôi một vuông góc và OA = OB =OC =6 Tính bán kính R của mặt cầu ngoại tiếp tứ diện OABC
A. R = 4 2
B. R = 2
C. R = 3
D. R = 3 3
Cho khối tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và OA OB OC 6. Tính bán kính R mặt cầu ngoại tiếp tứ diện OABC.
Đọc tiếp
Cho khối tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và OA = OB = OC = 6. Tính bán kính R mặt cầu ngoại tiếp tứ diện OABC.
![]()
![]()
![]()
![]()
Tứ diện OABC có OA = 1, OB = 2, OC = 3 và đôi một vuông góc với nhau. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA. Tính thể tích khối tứ diện OMNP
A. 1
B. 1 3
C. 1 4
D. 1 6
Cho tứ diện OABC có OA,OB,OC đôi một tạo với nhau góc và OA OB a, OC 2a. Côsin góc giữa đường thẳng OC và mặt phẳng (ABC) bằng A.
5
3
B.
1
3
C.
2
3
D.
2...
Đọc tiếp
Cho tứ diện OABC có OA,OB,OC đôi một tạo với nhau góc và OA = OB= a, OC =2a. Côsin góc giữa đường thẳng OC và mặt phẳng (ABC) bằng
A. 5 3
B. 1 3
C. 2 3
D. 2 2 3



