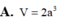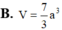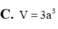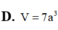Các câu hỏi tương tự
Cho
d
1
,
d
2
chéo nhau và khoảng cách
d
1
,
d
2
3
. Biết
d
1
∥
v
1
→...
Đọc tiếp
Cho d 1 , d 2 chéo nhau và khoảng cách d 1 , d 2 = 3 . Biết d 1 ∥ v 1 → = 2 ; - 1 ; 1 ; d 1 ∥ v 2 → = 1 ; 1 ; 2 ; A , B ∈ d 1 và C , D ∈ d 2 sao cho A B = C D = 2 . Biết tứ diện ABCD có thể tích V không phụ thuộc việc chọn các điểm A, B, C, D. Tính V.
![]()
![]()
![]()
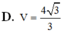
Cho tứ diện ABCD. Gọi B' và C' lần lượt là trung điểm của AB và AC. Tỉ số thể tích của khối tứ diện AB'C'D và khối tứ diện ABCD bằng:
A. 1/2 B. 1/4
C. 1/6 D. 1/8.
Trong không gian cho ABCD là hình chữ nhật,
A
B
2
,
A
D
1
. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết
d
A
B
,
d...
Đọc tiếp
Trong không gian cho ABCD là hình chữ nhật, A B = 2 , A D = 1 . Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d A B , d < d C D , d . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
![]()
![]()
![]()
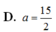
Cho tứ diện ABCD có
A
B
a
2
, ACADa, BCBDa, CDa. Tính thể tích V của khối tứ diện ABCD.
Đọc tiếp
Cho tứ diện ABCD có A B = a 2 , AC=AD=a, BC=BD=a, CD=a. Tính thể tích V của khối tứ diện ABCD.
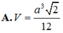
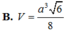
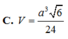
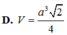
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc, AB 4 cm, AC 5 cm, AD 3 cm. Tính thể tích khối tứ diện ABCD. A. 20
c
m
3
B. 10
c
m
3
C. 15
c
m
3
D. 60
c
m
3
Đọc tiếp
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc, AB = 4 cm, AC= 5 cm, AD = 3 cm. Tính thể tích khối tứ diện ABCD.
A. 20 c m 3
B. 10 c m 3
C. 15 c m 3
D. 60 c m 3
Cho tứ diện ABCD có thể tích bằng V. Gọi B’ và D’ lần lượt là trung điểm của cạnh AB và AD. Mặt phẳng(CBD’) chia khối tứ diện thành hai phần. Tính theo V thể tích khối chóp C.B’D’DB? A.
3
V
2
B.
V
4
C.
V
2
D....
Đọc tiếp
Cho tứ diện ABCD có thể tích bằng V. Gọi B’ và D’ lần lượt là trung điểm của cạnh AB và AD. Mặt phẳng(CB'D’) chia khối tứ diện thành hai phần. Tính theo V thể tích khối chóp C.B’D’DB?
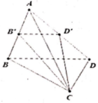
A. 3 V 2
B. V 4
C. V 2
D. 3 V 4
Hình thang vuông ABCD (như hình vẽ) có
A
B
3
a
2
,
A
D
a
,
D
^
60
o
. Cho ABCD quay quanh AB thành khối tròn xoay có thể tích V. Tính V.
Đọc tiếp
Hình thang vuông ABCD (như hình vẽ) có A B = 3 a 2 , A D = a , D ^ = 60 o . Cho ABCD quay quanh AB thành khối tròn xoay có thể tích V. Tính V.

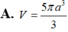
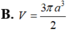
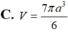

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
x
1
+
t
y
2
-
2
t
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 x = 1 + t y = 2 - 2 t z = - 3 - t và d 2 x = 4 + 3 t y = 3 + 2 t z = 1 - t . Trên đường thẳng d₁ lấy hai điểm A, B thỏa mã AB=3. Trên đường thẳng d₂ lấy hai điểm C, D thỏa mãn CD=4. Tính thể tích V của tứ diện ABCD.
A. V=7
B. V=2 21
C.V= 4 21 3
D.V= 5 21 6
Cho hình thang vuông ABCD đỉnh A và B có AB AD a, BC 2a. Cho hình thang ABCD quay quanh AB tạo thành 1 khối tròn xoay có thể tích V. Tính V
Đọc tiếp
Cho hình thang vuông ABCD đỉnh A và B có AB = AD = a, BC = 2a. Cho hình thang ABCD quay quanh AB tạo thành 1 khối tròn xoay có thể tích V. Tính V