ADOE là hình bình hành, lại có AO là đường phân giác của góc A nên là hình thoi.

ADOE là hình bình hành, lại có AO là đường phân giác của góc A nên là hình thoi.
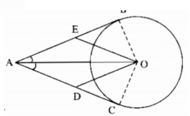
a) Từ điểm A nằm ngoài đtròn (O), kẻ cắc tiếp tuyến AB, AC với đtròn. Đường thẳng đi qua O và song song AB cắt AC ở D. Đường thẳng qua O và song song AC cắt AB ở E. Tứ giác ADOE là hình gì ?
b) Cho đường tròn (O) và đtròn (O') tiếp xúc ngoài tại A. Qua A kẻ đường thẳng bất kì cắt (O) tại C, cắt (O') tại D. Cm: OC // O'D.
c) Cho đtròn (O) và đtròn (O') cắt nhau tại 2 điểm A,B. Kẻ đường kính AC của đtròn (O) và đường kính AD của đtròn (O'). Cm:
1] CB // OO'.
2] Ba điểm B, C, D thẳng hàng.
Từ một điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm). Một đường thẳng (d) đi qua A cắt đường tròn (O) tại hai điểm D và E (d không đi qua tâm O, D nằm giữa A và E), gọi I là trung điểm của DE. BC cắt AE tại S. Qua C kẻ đường thẳng song song với AB, đường thẳng này cắt các đường thẳng BE, BD lần lượt tại M và N. CM: C là trung điểm MN.
Từ một điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm). Một đường thẳng (d) đi qua A cắt đường tròn (O) tại hai điểm D và E (d không đi qua tâm O, D nằm giữa A và E), gọi I là trung điểm của DE. BC cắt AE tại S. Qua C kẻ đường thẳng song song với AB, đường thẳng này cắt các đường thẳng BE, BD lần lượt tại M và N. CM: C là trung điểm MN.
Giúp mình bài này với.
cho đường tròn (O) và điểm A nằm ngoài đường tròn. Từ A kẻ các tiếp tuyến AB, AC(B, C là tiếp điểm). Qua B kẻ đường thẳng song song với AC cắt (O) tại E. AE cắt (O) tại D, BD cắt AC tại M. CHứng minh M là trung điểm của AC
Cho đường tròn (O;R), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn ( B, C là các tiếp điểm), gọi E là trung điểm của BC.
1. Cm A, E, O thẳng hàng và OE=R2
2. Qua điểm M thuộc cung nhỏ BC kẻ tiếp tuyến với đường tròn (O) , nó cắt các tiếp tuyến AB, AC thứ tự tại D và K. Cm chu vi tam giác ADK bằng 2AB.
3. Đường thẳng đi qua O song song BC cắt các đường thẳng AB , AC thứ tự P,Q. Cm DP + KQ >= PQ
Bài 8. (3,0 điểm) Từ điểm A ở ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC (B, C là hai tiếp điểm) và cát tuyến ADE (AD < AE). a) Chứng minh: OA BC và tứ giác ABOC nội tiếp. b) Đường thẳng đi qua điểm C, song song với DE và cắt đường tròn (O) tại F (F khác C). Gọi I là giao điểm của BF và DE. Chứng minh: I là trung điểm của DE. c) Chứng minh rằng: BE.EF + BD.DF = BC.DE.
1.Cho tam giác ABC có AD là tia phân giác trong của góc A. Quá D kẻ đường thẳng song song với AB cắt AC ở E và đường thẳng song song với AC cắt AB ở F.
a) Tứ giác AEDF là hình gì? Vì Sao?
b) Đường tròn đường kính AD cắt AB và AC lần lượt tại các điểm M và N. Chứng minh rằng: MN//EF.
2. Cho hai đường tròn (O;R) và(O';R') tiếp xúc trong với nhau tại A, (R>R'). Qua điểm B bất kỳ trên(O') vẽ tiếp tuyến với (O') cắt (O) tại hại điểm M và N, AB cắt (O) tại C. Chứng minh rằng:
a) MN vuông góc với OC
b) AC là tia phân giác của góc MAN
Cho (O; R) và một điểm A ở ngoài đường tròn sao cho OA = 3R. Từ A vẽ 2 tiếp tuyến AB,
AC đến (O) với B và C là các tiếp điểm.
a) Chứng minh tứ giác OBAC nội tiếp
b) Từ B vẽ đường thẳng song song với AC cắt (O) tại D. Đường thẳng AD cắt đường tròn
tại E và tia BE cắt AC tại F. Chứng minh rằng F là trung điểm của AC
c) Gọi H là giao điểm của BC và OA. Chứng minh rằng HB là tia phân giác của góc EHD.
Cho đường tròn (O). Từ điểm A bên ngoài đường tròn vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Đường thẳng kẻ qua C song song với AB cắt đường tròn (O) ở D, AD cắt đường tròn (O) ở M, CM cắt AB ở N. Chứng minh: a) Góc BAD = Góc ACN b) AN2 = NM.NC; c) N là trung điểm của AB.