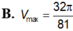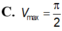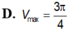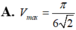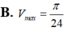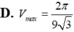Các câu hỏi tương tự
Xét các hình nón tròn xoay có đường sinh độ dài bằng 1 thì hình nón có thể tích lớn nhất
V
m
a
x
bằng bao nhiêu?
Đọc tiếp
Xét các hình nón tròn xoay có đường sinh độ dài bằng 1 thì hình nón có thể tích lớn nhất V m a x bằng bao nhiêu?
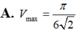
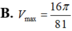
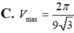
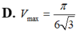
Trong tất cả các hình trụ mà tổng độ dài đường sinh và bán kính đường tròn đáy bằng 1 thì hình trụ có thể tích lớn nhất
V
m
a
x
bằng bao nhiêu?
Đọc tiếp
Trong tất cả các hình trụ mà tổng độ dài đường sinh và bán kính đường tròn đáy bằng 1 thì hình trụ có thể tích lớn nhất V m a x bằng bao nhiêu?
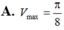
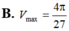
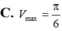
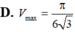
Cho hình nón tròn xoay có độ dài đường sinh là 2a, góc ở đỉnh của hình nón bằng
60
°
. Thể tích V của khối nón đã cho là
Đọc tiếp
Cho hình nón tròn xoay có độ dài đường sinh là 2a, góc ở đỉnh của hình nón bằng 60 ° . Thể tích V của khối nón đã cho là
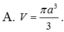
![]()
![]()
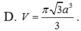
Một hình nón tròn xoay có độ dài đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng
9
π
. Khi đó đường cao hình nón bằng :
Đọc tiếp
Một hình nón tròn xoay có độ dài đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng 9 π . Khi đó đường cao hình nón bằng :
![]()
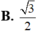
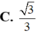
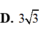
Một hình nón tròn xoay có độ dài đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng
9
π
.Khi đó đường cao hình nón bằng:
Đọc tiếp
Một hình nón tròn xoay có độ dài đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng 9 π .Khi đó đường cao hình nón bằng:
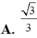
![]()
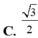
![]()
Một hình nón tròn xoay có độ dài đường sinh bằng đường kính đáy. Diện tích của hình nón bằng 9π. Khi đó đường cao của hình nón bằng:
A
.
3
B
.
3
3
C
.
3
2
D
.
3
3
Đọc tiếp
Một hình nón tròn xoay có độ dài đường sinh bằng đường kính đáy. Diện tích của hình nón bằng 9π. Khi đó đường cao của hình nón bằng:
A . 3
B . 3 3
C . 3 2
D . 3 3
Một hình nón tròn xoay có góc ở đỉnh bằng
120
o
, đường sinh bằng a. Tính thể tích V của hình nón
Đọc tiếp
Một hình nón tròn xoay có góc ở đỉnh bằng 120 o , đường sinh bằng a. Tính thể tích V của hình nón
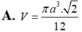
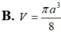
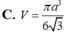
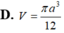
Biết góc ở đỉnh của một hình nón xoay bằng
120
o
, độ dài đường sinh bằng a. Tính thể tích V của hình tròn
Đọc tiếp
Biết góc ở đỉnh của một hình nón xoay bằng 120 o , độ dài đường sinh bằng a. Tính thể tích V của hình tròn
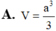
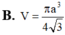
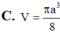
Hình nón tròn xoay nội tiếp trong mặt cầu bán kính
R
3
4
có thể tích lớn nhất bằng bao nhiêu
V
m
a
x
Đọc tiếp
Hình nón tròn xoay nội tiếp trong mặt cầu bán kính R = 3 4 có thể tích lớn nhất bằng bao nhiêu V m a x
![]()