Các câu hỏi tương tự
GIÚP EM VỚI Ạ. NGÀY MAI EM KIỂM TRA RỒI Ạ
Chứng minh rằng tập hợp các số thực có dạng a+b\(\sqrt{2}\) a,b\(\in\)Z với phép cộng thông thường là một nhóm Abel
Bài 1. Thực hiện các phép toán sau:
a/ (3+4i)+(-1+5i)
b/ (3-4i)-(1-5i)
c/ (-3+4i)+(1-4i)
d/ (3-5i)-(4+i)
Bài 2. Thực hiện các phép toán sau:
a/ (3+4i)(-1+5i)
b/ (3-5i)-(4+i)
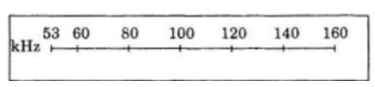
Trên mặt mỗi chiếc radio đều có các vạch chia để người sử dụng dễ dàng chọn đúng song radio cần tìm. Biết vạch chia ở vị trị cách vạch tâm cũng bên trái một khoảng d(cm) thì ứng với tần số Fk.ad(kHz), trong đó k và a là hai hằng số được chọn sao cho vạch tận cùng bên trái ứng với tần số 53kHz, vạch tậm cùng bên phải ứng với tần số 160kHz và hai vạch nàu cách nhau 12cm.a) Tính k và a (tính a chính xác đến hàng phần nghìn)b) Giả sử cho F, hãy giải thích Phương trình k.adF với ẩn d.c) Áp dụng kết q...
Đọc tiếp
Trên mặt mỗi chiếc radio đều có các vạch chia để người sử dụng dễ dàng chọn đúng song radio cần tìm. Biết vạch chia ở vị trị cách vạch tâm cũng bên trái một khoảng d(cm) thì ứng với tần số F=k.ad(kHz), trong đó k và a là hai hằng số được chọn sao cho vạch tận cùng bên trái ứng với tần số 53kHz, vạch tậm cùng bên phải ứng với tần số 160kHz và hai vạch nàu cách nhau 12cm.
a) Tính k và a (tính a chính xác đến hàng phần nghìn)
b) Giả sử cho F, hãy giải thích Phương trình k.ad=F với ẩn d.
c) Áp dụng kết quả của b, hãy điền vào ô trống trong bảng sau (kết quả chính xác
Hãy cho biết kết quả S của thuật toán nếu nhập n=4: Bước 1: Nhập n; Bước 2: Cho S=1, i=1; Bước 3: Kiểm tra nếu i<=n thì thực hiện bước 4, ngược lại thực hiện bước 6; Bước 4: S=S + i ; Bước 5: Tăng i lên 1 đơn vị và quay lại bước 3; Bước 6: In S và kết thúc chương trình.
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Cho hàm số
f
x
log
1
2
log
4
log
1
4
log
16
log...
Đọc tiếp
Cho hàm số f x = log 1 2 log 4 log 1 4 log 16 log 1 16 x . Tập xác định của f(x) là D=(a;b) trong đó a và b là các số thực, b − a = m n , m và n là các số tự nhiên nguyên tố cùng nhau. Tìm tổng m + n.
A. 19
B. 31
C. 271
D. 319
chỉ mik cách lập nhóm nhaTrích một số bài toán trong đề:+ Trên mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa mãn điều kiện /z/ 2 là:A. Đường tròn tâm O, bán kính R 2B. Đường tròn tâm O, bán kính R 4C. Đường tròn tâm O, bán kính R 1/2D. Đường tròn tâm O , bán kính R căn 2+ Cho hàm số y f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?A. Hàm số y f(x) có giá trị cực đại bằng 0B. Giá trị lớn nhất của hàm số y f(x) trên tập R là 1C. Hà...
Đọc tiếp
chỉ mik cách lập nhóm nha
Trích một số bài toán trong đề:
+ Trên mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa mãn điều kiện /z/ = 2 là:
A. Đường tròn tâm O, bán kính R = 2
B. Đường tròn tâm O, bán kính R = 4
C. Đường tròn tâm O, bán kính R = 1/2
D. Đường tròn tâm O , bán kính R = căn 2
+ Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số y = f(x) có giá trị cực đại bằng 0
B. Giá trị lớn nhất của hàm số y = f(x) trên tập R là 1
C. Hàm số y = f(x) đạt cực đại tại x = 0 và cực tiểu tại x = -1
D. Hàm số y = f(x) có đúng một cực trị
+ Tìm phần thực của số phức (2 + 3i).i^10
2.trong tập \(R\times R=R^2\) ,với R là tập số thực,ta xác định một quan hệ hai ngôi S như sau: (x1,y1)S(x2,y2) <=>x1=x2
a.chứng minh rằng S là một quan hệ tương đương trong \(^{R^2}\)
b.xác định lớp tương đương C(a,b) với a, b là 2 số tùy ý.
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số