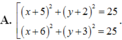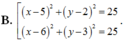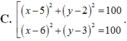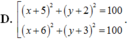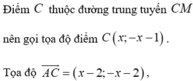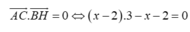Các câu hỏi tương tự
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-50. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-5=0. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
![]()
![]()
![]()
![]()
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có
M
(
2
;
0
)
là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là
7
x
-
2
y
-
3
0
và
6
x
-
y
-
4
0
. Phương trình đường thẳng AC...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có M ( 2 ; 0 ) là trung điểm của cạnh AB. Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7 x - 2 y - 3 = 0 và 6 x - y - 4 = 0 . Phương trình đường thẳng AC là
A. 3 x - 4 y - 5 = 0
B. 3 x + 4 y + 5 = 0
C. 3 x - 4 y + 5 = 0
D. 3 x + 4 y - 5 = 0
Trong mặt phẳng tọa độ Oxy, cho điểm A (-1;3) và đường thẳng ∆ có phương trình là x – 2y + 2 0. Dựng hình vuông ABCD sao cho hai đỉnh B, C nằm trên ∆. Tìm tọa độ điểm C biết C có tung độ dương A. C (-2;0) B. C (0;1) C. C(2;2) D. C(1;4)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho điểm A (-1;3) và đường thẳng ∆ có phương trình là x – 2y + 2 = 0. Dựng hình vuông ABCD sao cho hai đỉnh B, C nằm trên ∆. Tìm tọa độ điểm C biết C có tung độ dương
A. C (-2;0)
B. C (0;1)
C. C(2;2)
D. C(1;4)
Trong hệ tọa độ
O
x
y
cho tam giác
A
B
C
có phương trình đường thẳng
B
C
:
x
+
7
y
-
13
0
. Các chân đường cao kẻ từ
B
,
C
lần lượt là
E
(
2
;
5
)
,...
Đọc tiếp
Trong hệ tọa độ O x y cho tam giác A B C có phương trình đường thẳng B C : x + 7 y - 13 = 0 . Các chân đường cao kẻ từ B , C lần lượt là E ( 2 ; 5 ) , F ( 0 ; 4 ) Biết tọa độ đỉnh A là A ( a ; b ) Khi đó:
A. a - b = 5
B. 2 a + b = 6
C. a + 2 b = 6
D. b - a = 5
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có
A
(
-
1
;
3
;
2
)
;
B
(
2
;
0
;
5
)
;
C
(
0
;
-
2
;
1
)
.
Phương trình đường trung tuyến AM của tam giác ABC là. A.
x
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A ( - 1 ; 3 ; 2 ) ; B ( 2 ; 0 ; 5 ) ; C ( 0 ; - 2 ; 1 ) . Phương trình đường trung tuyến AM của tam giác ABC là.
A. x - 1 - 2 = y + 3 4 = z + 2 - 1
B. x - 1 2 = y + 3 - 4 = z + 2 1
C. x + 1 2 = y - 3 - 4 = z - 2 1
D. x - 2 1 = y + 4 - 1 = z + 1 3
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có
A
(
-
1
;
3
;
2
)
;
B
(
2
;
0
;
5
)
;
C
(
0
;
-
2
;
1
)
.
Phương trình đường trung tuyến AM của tam giác ABC là. A.
x
-
1
-
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A ( - 1 ; 3 ; 2 ) ; B ( 2 ; 0 ; 5 ) ; C ( 0 ; - 2 ; 1 ) . Phương trình đường trung tuyến AM của tam giác ABC là.
A. x - 1 - 2 = y + 3 4 = z + 2 - 1
B. x - 1 2 = y + 3 - 4 = z + 2 1
C. x + 1 2 = y - 3 - 4 = z - 2 1
D. x - 2 1 = y + 4 - 1 = z + 1 3
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có
A
(
2
;
1
;
-
2
)
;
B
(
4
;
-
1
;
1
)
v
à
C
(
0
;
-
3
;
1
)
.
Phương trình d đi qua trọng tâm của tam giác ABC và vuông góc v...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A ( 2 ; 1 ; - 2 ) ; B ( 4 ; - 1 ; 1 ) v à C ( 0 ; - 3 ; 1 ) . Phương trình d đi qua trọng tâm của tam giác ABC và vuông góc với mặt phẳng (ABC) là
A. x = 2 + t y = - 1 - 2 t z = - 2 t
B. x = - 2 + t y = - 1 - 2 t z = - 2 t
C. x = 2 + t y = 1 - 2 t z = - 2 t
D. x = 2 + t y = 1 + 2 t z = 2 t
Trong không gian tọa độ Oxy cho tam giác ABC biết A(1;0;-1), B(2;3;-1), C(-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp cảu tam giác ABC và vuông góc với mặt phẳng (ABC). A.
x
-
3
3
y
-
1
-...
Đọc tiếp
Trong không gian tọa độ Oxy cho tam giác ABC biết A(1;0;-1), B(2;3;-1), C(-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp cảu tam giác ABC và vuông góc với mặt phẳng (ABC).
A. x - 3 3 = y - 1 - 1 = z - 5 5
B. x 3 = y - 2 1 = z 5
C. x - 1 1 = y - 2 = z + 1 2
D. x - 3 3 = y - 2 1 = z 5
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:x-y-30 và điểm A(2;6). Trên đường thẳng d lấy hai điểm B và C sao cho tam giác ABC vuông tại A và có diện tích bằng
35
2
2
. Phương trình đường tròn ngoại tiếp tam giác ABC là:
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:x-y-3=0 và điểm A(2;6). Trên đường thẳng d lấy hai điểm B và C sao cho tam giác ABC vuông tại A và có diện tích bằng 35 2 2 . Phương trình đường tròn ngoại tiếp tam giác ABC là: